Two heavy metallic plates are joined together at `90^@` to each other. A laminar sheet of mass 30kg is hinged at the line AB joining the two heavy metallic plates. The hinges are frictionless. The moment of inertia of the laminar sheet about an axis parallel to AB and passing through its center of mass is 1.2 kg `m^2.` Two rubber obstacles P and Q are fixed, one on each metallic plate at a distance 0.5m from the line AB. This distance is chosen so that the reaction due to the hinges on the laminar sheet is zero during the impact. Initially the laminar sheet hits one of the obstacles with an angular velocity 1 rad/s and turns back. If the impulse on the sheet due to each obstacle is 6 N-s,
(a) Find the location of the center of mass of the laminar sheet from AB.
(b) At what angular velocity does the laminar sheet come back after the first impact?
(c) After how many impacts, does the laminar sheet come to rest?

Answer

A, B, C, D

Explanation

`I_c =1.2kg- m^2`

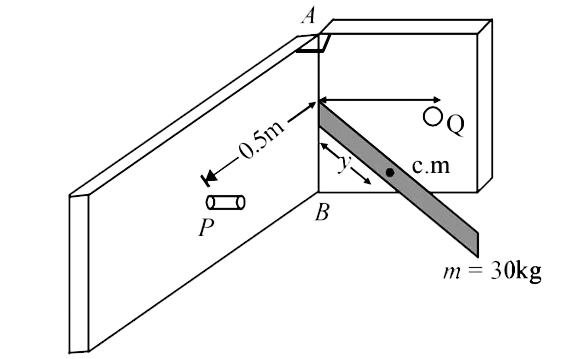
Let y be the distance of c.m. from line AB.
Applying parallel axis theorem of M.I. we get
M.I. of lamiar sheet about AB
`I_(AB) = I_(c.m.) +my^2`
`I_(AB)=12 + 30y^2 …..(i)`
The angular velocity of the laminar sheet will change after
impulse = Change in linear momentum
`6 =30(v_f - V_i)`
`6= 30 xxy(omega_f - omega_i)..(ii)`
Also, change in angular momentum = Moment of impulse
`:. I_(AB) omega_f - I_(AB)omega_i = impulse xx distance`
`I_(AB)(omega_f - omega_i) = 6xx0.5 = 3`
`:. omega_f = (3)/(I_(AB) + omega_i = (3)/(1.2 + 30y^2 + (-1) ...(iii)`
Note: Minus sign with `omega_i` because the direction of laminar
plate towards the obstacle is taaken as - ve (assumption).
From (ii) and (iii)`
`6 = 30 xxy [(3)/(1.2+30y^2)-1+1]`
`1 = 5y[(3)/(1.2 + 30y^2]`
`:. 1.2 +30y^2 = 5y[+3] = 15y`
`:. 30yk^2 - 15y - 1.2 = 0`
On solving we get y = 0.1 or 0.4
`:. omega_f = 1red/s if we puty y = 0.1 in eq. (ii)`
And `oemga_f = 0.5 rad/s if we put y = 0.4 in eq. (ii)`
(Not valid as per sign convention)
Now, since the lamina sheet comes back with same angular
speed as that of incident angular speed, the sheet will sming
in between P and Q infinitely.