Three particles A, B and C each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l. This body is placed on a horizonta frictionsess table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A . the body is set into rotational motion on the table about A with a constant angular velocity `omega`.

(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.

Answer

A, B, C, D

Explanation

(a) The mass B is moving
in a ciruclar path centred at
A. The centripetal force
`(m l omega^2)`required for this
circular motion is provided by
F'. Therefore a force F' acts
on A (the hinge) which is
equal to `m I omega^2.` The same is the case for mass C.
Therefore the net force on the
hinge is

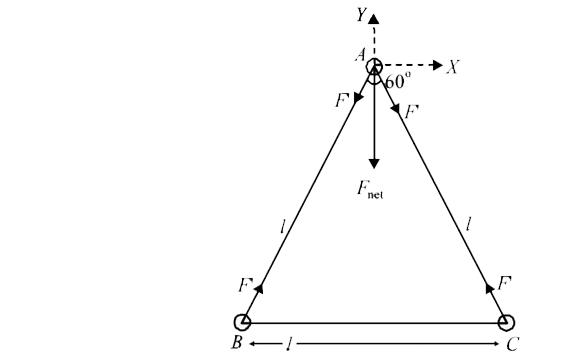
`F_(net) = sqrt(F'^2 +F^2 + 2F' F' cos 60^@)`
`F_(net) =sqrt(2F'^2 + 2F'^2 xx(1)/(2)) = sqrt3F' =sqrt3 l omega^2`
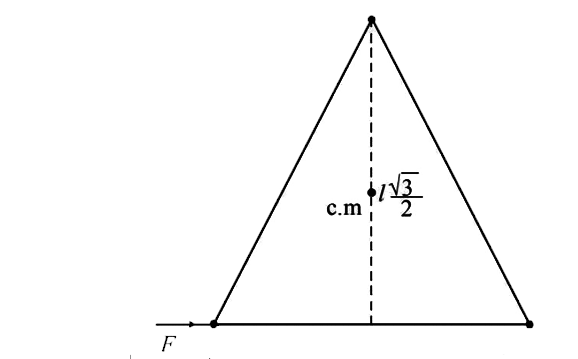
(b) The force F acting on B Will probide a torque to the system. This torque is `Fxx (lsqrt3)/(2) = Ialpha`
`Fxx(xsqrt3l)/(2) = (2ml^2)alpha`
`rArr alpha = (sqrt3)/(4)xx((F)/(ml))`

The total force acting on the system along x-direction is
`F + (F_(net)_x`
This force is responsible for giving an acceleration `a_x` to the system.
Therefore,
`F+(F_(net))_x = 3m(a_x)_cm.`
`=3m(F)/(4m) (:. alpha_x =alphar = (sqrt3)/(4) (F_)/(ml)xx(l)/(sqrt3) = (F)/(4))``
`(3F)/(4) :. (F_net) = - (F)/(4)`
`(F_(net))_y remains the same as before = sqrt3mlomega^2.`