A cylinder of mass m and radius R rolls down an inclined plane of inclination `theta`. Calculate the linear acceleration of the axis of cylinder.

Answer

A, B, C

Explanation

Applying `F_(net) =main X-direction
`mg sin theta-f =ma…(i)`
The torque about O will be
`tau = fxxR`
`=Ialpha …(ii)`
As the case is of rolling
`:. a =alphaR`
`rArr alpha = (a)/(R )…..(iii)`

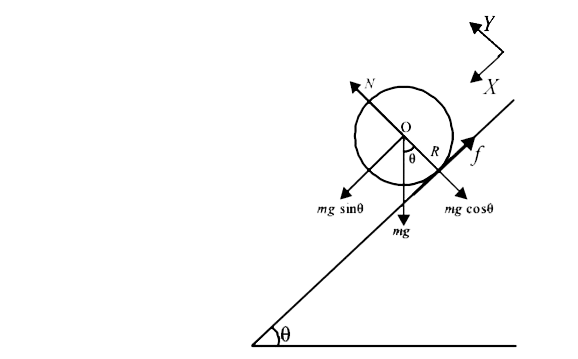
From (ii) and (iii), f = (la)/(R^2)`
Substituting this value in (i), we get
`mg sin theta - (Ialpah)/(R^2) -= ma`
`rArr a= (mgsintheta)/(m+(I)/(R^2) = (mgsintheta)/(m+(1)/(2)(mR^2)/(R^2) = (2)/(3)g sin theta`
`[:. I = (1)/(2)mR^2 for solid cylinder ]`