A boy is pushing a ring of mass 2kg and radius 0.5 m with a stick as shown in figure. The stick applies a force of 2N on the ring and rolls it without slipping with an acceleration of `0.3 m/s^2.` The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the ring of (P/10). The value of P is

Answer

D

Explanation

Under the influence of the force of stick (2N), the point of
contact O of the ring with ground tends to slide. But the
frictional force `f_2` does not allow this and cretes a torque
which starts rolling the ring. A frictjion forve `f_1` also acts
between the ring & the stick.
Applying `F_(net) = ma` in the horizontal direction. We get

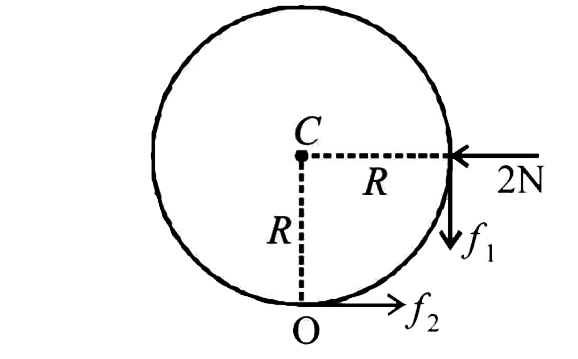
`2-f_2 = 2xx0.3 ` :. f_2 = 1.4N`
Applying `tau = I alpha about C we get
`(f_2- f_1) R= Ialpha = I(alpha)/(R ) [:. For rolling a= Ralpha]`
`:. [1.4 - muxx2]xx0.5 = 2xx(0.5)^2xx(0.3)/(0.5) [ :. I = MR^2]`
`:. mu = 0.4`
Given mu = (P)/(10) :. P =4`