From a solid sphere of M and radius R a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendiular to one of its faces is:

Options

A. `(4MR)^2/(9sqrt3pi)`
B. `(4MR)^2/(3sqrt3pi)`
C. `(MR)^2/(32sqrt2pi)`
D. `(MR)^2/(16sqrt2pi)`

Answer

A

Explanation

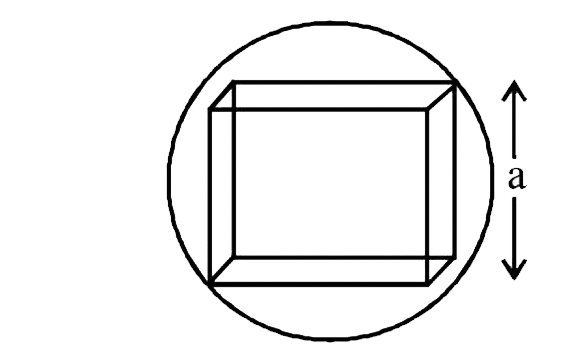
(a) Here `a =(2)/(sqrt3)R`
`Now , (M)/(M') = ((4)/(3)prR^2)/(a^3)`
`=((4)/(3)piR^3)/((2)/(sqrt3)R)^3 = (sqrt3)/(2) pi, M' =(2M)/(sqrt3pi)`
Moment of inertia of the given axis,
`I = (M'a^2)/(6) = ((2M)/(sqrt3pi)xx((2)/(sqrt3)R))^2)/(6) = (4MR^2)/(9sqrt3pi)`