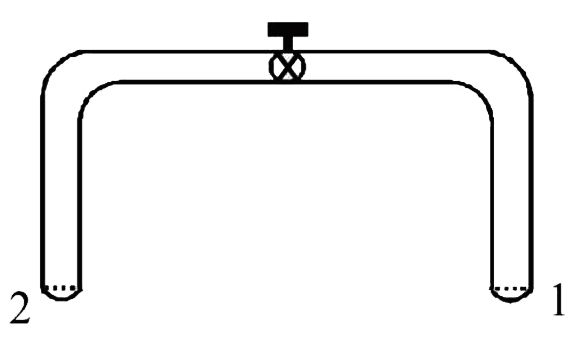
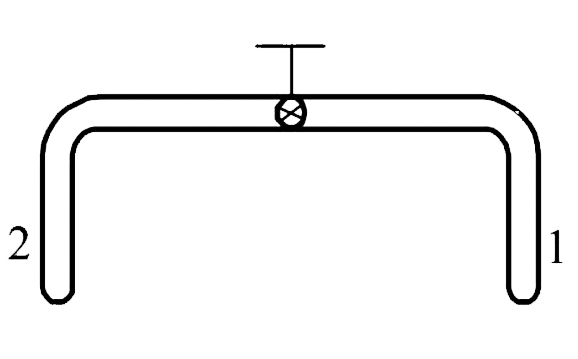
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MECHANICAL PROPERTIES OF MATTER AND FLUIDS
SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise Subjective Problems|1 VideosLAWS OF MOTION
SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise JEE Main And Advanced|79 VideosMOMENTUM & IMPULSE
SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise JEE Main And Advanced|30 Videos
Similar Questions
Explore conceptually related problems