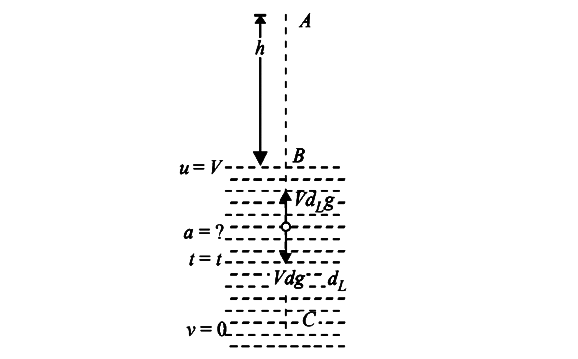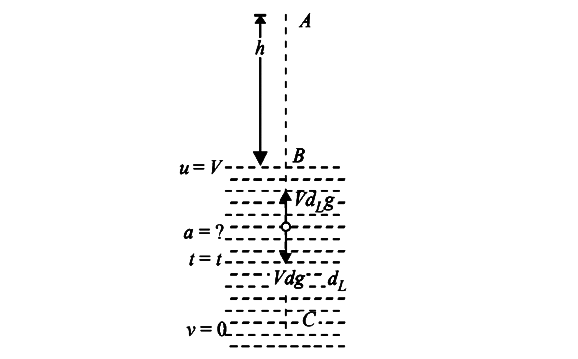A ball of density d is dropped on to a horizontal solid surface. It bounces elastically from the surface and returns to its original position in a time `t_1`. Next, the ball is released and it falls through the same height before striking the surface of a liquid of density of `d_L`
(a) If `dltd_L`, obtain an expression (in terms of d, `t_1` and `d_L`) for the time `t_2` the ball takes to come back to the position from which it was released.
(b) Is the motion of the ball simple harmonic?
(c) If `d=d_L`, how does the speed of the ball depend on its depth inside the liquid? Neglect all frictional and other dissipative forces. Assume the depth of the liquid to be large.

Answer

A, B, C, D

Explanation

Let the ball be dropped from a height h. During fall `V=ut+at=0+gt_1/2impliest_1=(2v)/(g)`
In the second case the ball is made to fall through the same height and then the ball strikes the surface of liquid of density `d_L`. When the ball reaches inside the liquid, it is under the influence of two force (i) `Vdg`, the weight of ball in downward direction (ii) `Vd_Lg`, the upthrust in upward direction.
The viscous forces are absent. (given)
Since, `d_Lgtd`
the upward force is greater and the ball starts retarding.
For motion B to C
`u=V`, `v=0`, `t=t`, `a=-a`
`v=u+at=0=v+(-a)t`
`impliest=v/a`
Now, `a=F_(n et)/(m)`
`=(Vd_Lg-Vdg)/(Vd)=((d_L-d)g)/(d)`
`impliest=(vd)/((d_L-d)g)` ...(iii)
Therefore,
`t_2=t_1+2t=t_1+(2dv)/((d_L-d)g)`
`=t_1+(2d)/((d_L-d)g)(t_1g)/(2)=t_1[1+(d)/(d_L-d)]`
`impliest_2=(d_Lt_1)/(d_L-d)`
(b) Since the retardation is not proportional to displacement, the motion of the ball is not simple harmonic.
(c) If `d=d_L` then the retardation `a=0`. Since the ball strikes the water surface with some velocity, it will continue with same velocity in downward direction(until it is interrupted by some other force).