A container of large uniform cross-sectional area A resting on a horizontal surface, holds two immiscible, non-viscous and incompressible liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure `P_0`.

(a) A homogeneous solid cylinder of length `L(LltH//2)`, cross-sectional area `A//5` is immersed such that it floats with its axis vertical at the liquid-liquid interface with length `L//4` in the denser liquid. Determine:
(i) the density D of the solid and
(ii) the total pressure at the bottom of the container.
(b) The cylinder is removed and the original arrangement is restored. A tiny hole of area `s(slt ltA)` is punched on the vertical side of the container at a height `h(hltH//2)`. Determine:
(i) the initial speed of efflux of the liquid at the hole,
(ii) the horizontal distance x travelled by the liquid initially, and
(iii) the height `h_m` at which the hole should be punched so that the liquid travels the maximum distance `x_m` initially. Also calculate `x_m`.

Answer

A, B, C, D

Explanation

(a) (i)
KEY CONCEPT:
Since the cylinder is in equilibrium in the liquid therefore
Weight of cylinder=upthrust
`mg=F_(T_1)+F_(T_2)` where
`F_(T_1)` and `F_(T_2)` = upthrust due to lower and upper liquid respectively

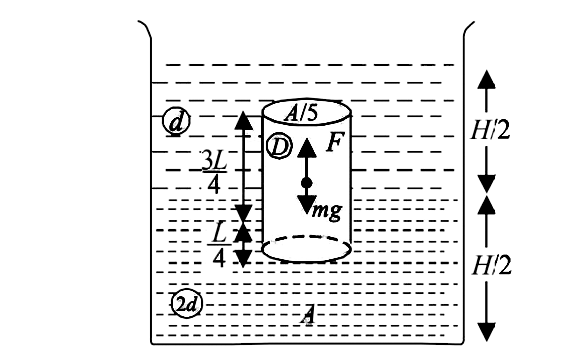
`A/5xxLxxDxxg=A/5xxL/4xx2d xx g+A/5xx(3L)/(4)xxd xxg`
`impliesD=(2d)/(4)+(3d)/(4)=(5d)/(4)`
(ii) Total pressure at the bottom of the cylinder=
Atmospheric pressure + Pressure due to liquid of density d+ Pressure due to liquid of density `2d+`
Pressure due to cylinder [Weight/Area]
`P=P_0+H/2dg+H/2 xx 2d xx g+ (A/5xxLxxDxxg)/(A)`
`impliesP=P_0+((3H)/(2)+(L)/(4))dg` `[:'D=(5d)/(4)]`
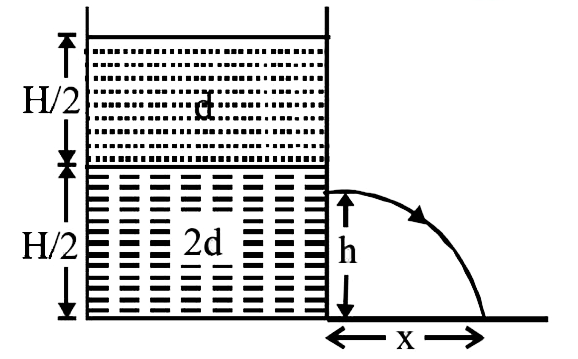
(b) KEY CONCEPT:
Applying Bernoulli's theorem
`P_0+[H/2xxd xxg+(H/2-h)2d xxg]`
`=P_0+1/2(2d)v^2impliesv=sqrt((3H-4h)/(2))g`
Horizontal Distance x
`u_x=v`, `t=t`, `x=vt` ...(i)
For vertical motion of liquid falling from hole
`u_y=0`, `S_y=h`, `a_y=g`, `t_y=t`
`S=ut+1/2at^2`
`impliesh=1/2gt^2impliest=sqrt((2h)/(g))` ...(ii)
`
From (i) and (ii)
`x=v_yxxsqrt((2h)/(g))=sqrt((3H-4h)g/2)xxsqrt((2h)/(g))`
`=sqrt((3H-4h)h)` ...(iii)
For finding the value of h for which x is maximum, we differentiate equation (iii) w.r.t. t
`(dx)/(dt)=1/2[(3H-4h)h]^(-1//2){3H-8h}`
Putting `(dx)/(dt)=0` for finding values h for maxima/minima
`1/2[(3H-4h)]^(-1//2)[3H-8h]=0impliesh=(3H)/(8)`
`:. x_m=sqrt([3H-4((3H)/(8))](3H)/(8))` [From (iii)]
`=sqrt((12H)/(8)xx(3H)/(8))=(6H)/(8)=(3H)/(8)`