A particle of mass `m = 1.6 X 10^(-27)` kg and charge `q = 1.6 X 10^(-19)` C moves at a speed of `1.0 X10^7 ms^(-1)`. It enters a region of uniform magnetic field at a point E, as shown in The field has a strength of 1.0 T. (a) The magnetic field is directed into the plane of the paper. The particle leaves the region of the filed at the point F. Find the distance EF and the angle theta. (b) If the field is coming out of the paper, find the time spent by the particle in the regio the magnetic feld after entering it at `E`.

Answer

A, C, D

Explanation

`m = 1.6xx10^(-27) kg, q = 1.6xx10^(-19)C`
`B = 1 T`
` v = 10^(7) m//s`
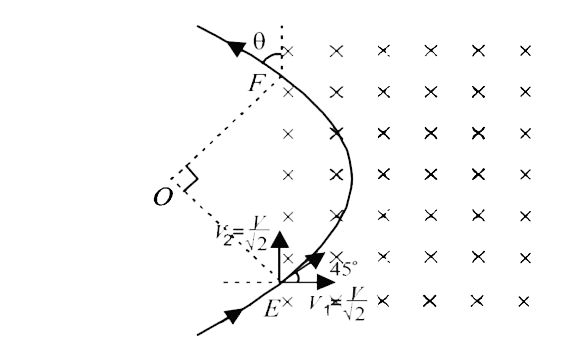
`F = q .v B sin alpha`
(acting towards ` O` by Fleming's left hand rule )
rArr ` F = qvB` `[:. alpha = 90^(@)]`
But ` F = ma`
:. ` qvB = ma :. a = (qvB)/(m)`
` = (1.6xx10^(-19)xx10^(7)xx1)/(1.6xx10^(-27)`
` = 10^(15) m//s^(2)`
`/_OEF = 45^(@)` ` (because OE act as a radius)`
By symmetry `/_OFE = 45^(@)`
:. `/_EOF = 90^(@)` ( by Geometry)
This is the centripetal acceleration
:. `(v^(2))/(r) = 10^(15) rArr r = (10^(14))/(10^(15)) = 0.1 m`.
Therefore ` EF = 0.141 m`.
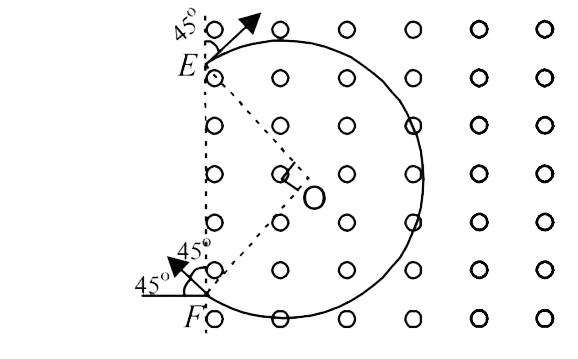
If the magnetic field is in the outward direction and the particle enters in the same way at `E` , then according to Fleming's left hand rule, the particle will turn towards clockwise direction and cover `3//4th` of a circle as shown in the figure.
Time required `= (3)/(4)xx [(2 pir)/(v)] = 4.71xx10^(-8) sec`.