Home
Class 12
PHYSICS
Two long parallel wires carrying current...

Two long parallel wires carrying current ` 2.5 amperes` and `I ampere` in the same direction ( directed into the plane of the paper) are held at `P and Q` respectively such that they are perpendicular to the plane of paper. The points `P and Q` are located at a distance of ` 5 metres and 2 metres` respectively from a collinear point `R` ( see figure)
(i) An electron moving with a velocity of ` 4xx10^(5) m//s ` along the positive ` x- direction ` experiences a force of magnitude `3.2xx10^(-20) N` at the point `R`. Find the value of `I`.
(ii) Find all the positions at which a third long parallel wire carrying a current of magnitude `2.5 amperes` may be placed so that the magnetic induction at `R` is zero.

Text Solution

Verified by Experts

The correct Answer is:
A, B, C, D
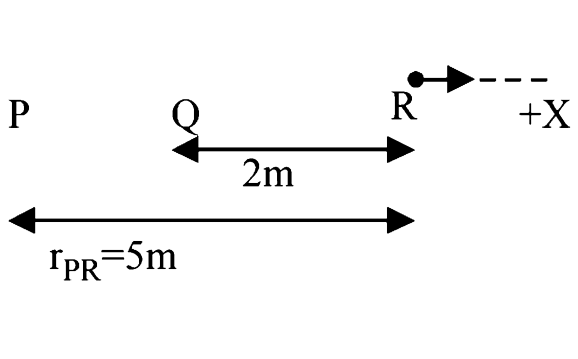
(i) The magnetic field (due to current in wire `P`) at `R`
` = (mu_(0))/( 4 pi ) xx(2I_(p))/(r_(PR)) = ( mu_(0))/( 4 pi)xx( 2xx2.5)/(5)`` = (mu_(0))/(4 pi)`
` = (mu_(0))/(4 pi) [ in the plane of paper downwards]`
Similarly , the magnetic field ( due to current is wire `Q`) ar `R`
`(mu_(0))/( 4 pi)xx( 2xxI)/(2) = (mu_(0))/( 4 pi)I`
`[ in the plane of paper downwards]`
The total magnetic field at `R [ due to `P and Q`]`
` B = (mu_(0))/( 4 pi )+(mu_(0))/( 4 pi)I = ( mu_(0))/( 4 pi) (1 + I)`
`[ in the plane of paper downwards ]`
The force experienced by the electron
` F = qvB sin theta`
` = evB sin 90^(@) = 1.6xx10^(-19)xx4xx10^(5)xx(mu_(0))/( 4 pi) ( 1+I)`
But ` F = 3.2xx10^(-20) N (Given)
:. `3.2xx10^(-20) = 1.6xx10^(-19)xx4xx10^(5)xx10^(-7)(1+I)`
rArr `I = 4 amp`.
(ii) Let us consider a position between ` Q and R` . The magnetic field produced should be equal to ` 5xx10^(-7)T` in the plane of paper acting upwards.
For this let the wire having current `2.5 amp` be placed at a distance `r` from ` R` and current flowing outwards the plane of paper. ltbr gt :. ` 5xx10^(-7) = (mu_(0))/(4 pi) xx( 2xx2.5)/(r) or r = 1 m`
Let us consider another position beyond ` R` collinear with `P, Q and R`. Let it be placed at a distance `r'' from `R' , having current in the plane of paper.
:. ` 5xx10^(-7) = (mu_(0))/(4 pi)xx( 2xx2.5)/(r') or r' = 1 m`
Promotional Banner

Topper's Solved these Questions

  • MOVING CHARGES AND MAGNETISM

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise MCQs(d )|1 Videos

  • MODERN PHYSICS

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise MCQ (One Correct Answer|1 Videos

  • RAY AND WAVE OPTICS

    SUNIL BATRA (41 YEARS IITJEE PHYSICS)|Exercise JEE Main And Advanced|209 Videos

Similar Questions

Explore conceptually related problems

Two long parallell wires carrying currents 2.5 A and I (ampere) in the same directon (directed into theplane of the paper) are held at P and Q , respectively such that they are perpendicular to the plane of paper. The points P and Q are located at distance of 5 m and 2m respectively from a collinear point R (see figure). a. An electron moving with a velocity of 4xx10^5 m/s along the positive x-directionn experieces a force of magnitude 3.2xx10^-20 N at the point R . Find the volume of I . b. Find all the positions at which a third long paralle wire carryig a current of magnitude 2.5 AS may be placed, so that the magnetic induction at R is zero.

In the adjoining diagram, P and Q are parallel wires carrying currents of 2.5 A and I respectively directed at right angles to the plane of paper inwards. An electron moving with velocity 4xx10^(5)m//s in positive x - direction experiences a force of 3.2xx10^(-20)N at point R. The value of i will be

Two long parallel conductors carry currents i_(1)=3A and i_(2)=3A both are directed into the plaane of paper. The magnitude of resultant magnetic field at point 'P' , is

Two infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is

Two particles p and q located at distances r_p and r_q respectively from the centre of a rotating disc such that r_p gt r_q .

Two long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is

Two thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will

Two long parallel wires placed 0.08 m apart, carry currents 3 A and 5 A in the same direction. what is the distance from the conductor carrying the larger current to the point where the resultant magnetic field is zero?

P, Q and R long parallel straight wires in air, carrying currents as shown. The direction of resultant force on R is :-