A uniform constant magnetic field `B` is directed at an angle of `45^(@)` to the `x axis` in the ` xy`- plane . ` PQRS` is a rigid, square wire frame carrying a steady current `I_(0)`, with its centre at the origin `O`. At time ` t = 0`, the frame is at rest in the position as shown in figure , with its sides parallel to the ` x and y` axis. Each side of the frame is of mass `M` and length `L`.
(a) What is the torque `tau` about `O` acting on the frame due to the magnetic field?
(b) Find the angle by which the frame rotates under the action of this torque in a short interval of time `Deltat`, and the axis about this rotation occurs .`( Deltat is so short that any variation in the torque during this interval may be neglected .) Given : the moment of interia of the frame about an axis through its centre perpendicular to its about an axis through its centre perpendicular to its plane is `(4)/(3) ML^(2)`.

Answer

A, B

Explanation

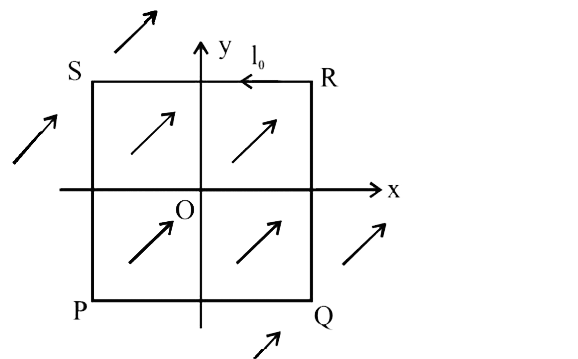
(a) As the magnetic field ` vec(B)` is in ` x-y` plane and subtents an angle of ` 45^(@)` with the `x- axis` , hence ,
`B_(x) = B cos 45^(@) = B//sqrt(2)` and
`B_(y) = B sin 45^(@) = B//sqrt(2)`
so , in vetor from
vec(B) = hat(i)((B)/(sqrt(2)))+ hat(j)((B)/(sqrt(2))) and vec(M) = I = I_(0)L^(2) hat(k)`
So, ` vec(tau) = vec(M)xxvec(B) = I_(0) L^(2) hat(k) xx((B)/(sqrt(2)) hat(i)+ (B)/(sqrt(2)) hat(j)) = (I_(0) L^(2) B)/sqrt(2) ( hat(j) - hat(i))`
i.e, torque has magnitude ` I_(0)^(2) L^(2) B` and is directed along line ` Qs from Q to S`.
(b) According to the therom of perpendicular axes, moment of interia of the frame about `Qs`.
` I_(QS) = (1)/(2)I_(z) = (1)/(2) ((4)/(3) ML^(2)) = (2)/(3) ML^(@)`
` tau = I alpha`,
:. ` alpha = (tau)/(I) = ( I_(0) L^(2)Bxx3)/( 2 ML^(2)) = (3)/(2) ( I_(0)B)/(M)`

Here `alpha` is constant , therefore we can apply
` theta = omega_(0) t + (1)/(2) alpha t^(2)` with ` omega_(0) = 0 `, we have
`theta = (1)/(2) alpha t ^(2) = (1)/(2) (( 3 I_(0) B)/( 2 M)) ( Delta t)^(2)`
or ` theta = (3)/(4) ( I_(0) B)/(M) ( Delta t)^(2)`