The region between ` x=o and x = L` is filled with uniform, steady magnetic field `B_(0) hat(k)`. A particle of mass `m` , positive charge `q` and velocity `v_(0) hat(i)` travels along ` x-axis` and enters the region of the magnetic field. Neglect gravity throughout the question .
(a) Find the value of `L` if the particle emerges from the region of magnetic field with its final velocity at angle `30^(@)` to its initial velocity.
(b) Find the velocity of the particle and the time spent by it in the magnetic field, if the magnetic field now extends upto `2.1L`.

Answer

A, B, C, D

Explanation

KEY CONCEPT : This question involves a simple understating of the motion of charged particle in a magnetic field.
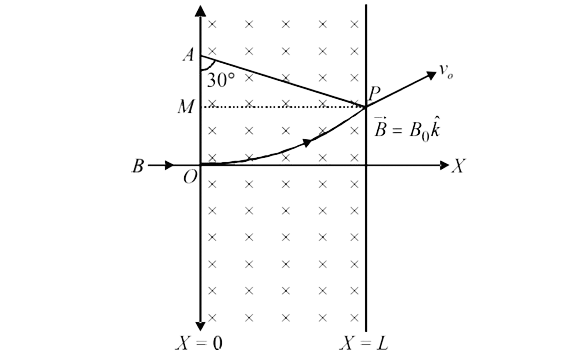
(a) Let the particle emerge out from the region of magnetic field at point `P`. Then the velocity vector `vec(v)_(0)` makes an angle `30^(@)` with ` x- axis `. The normal to circular path at `P` intersects the negative `y- axis ` at point `A`.
Hence, `AO = AP = R = radius of circular path , which can be found as
`(mv_(0)^(2))/(R) = B_(0)qv_(0) rArr R = (mv_(0))/(q^(B)_(0))` .....(i)
In ` Delta APM`, ` R sin 30^(@) = L rArr (R)/(2) = L` ....(ii)
From (i) and (ii) , `L = (mv_(0))/(2qB_(0))`
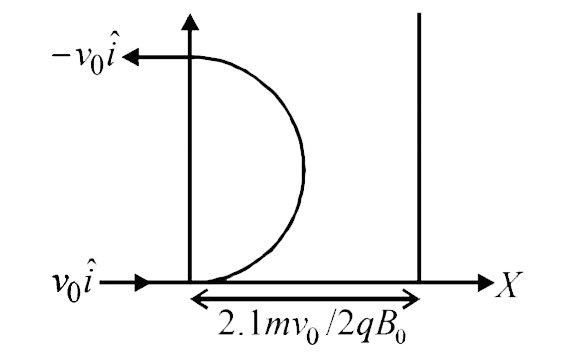
(b) As the new region of magnetic field is `2.1 L`
` = (2.1 R)/(2)` which is obviously `gt R` .
Thus, the required velocity `= -v_(0) hat(i)`.
Since the time taken period for complete revolution `= 2 pim//qB_(0)`. ,brgt The time taken by the particle to cross the region of magnetic field `= pim//qB_(0)`.