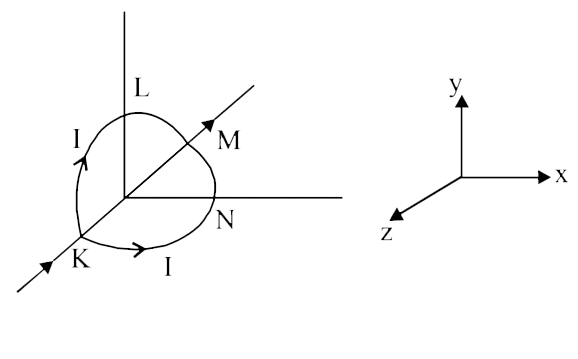
A circular loop of radius `R` is bent along a diameter and given a shapes as shown in the figure. One of the semicircles `(KNM)` lies in the ` x-z` plane with their centres and the other one `(KLM)` in the `y-z` plane with their centres at the origin. current `I` is flowing through each of the semi circles as shown in figure.
(a) A particle of charge `q` is released at the origin with a velocity `vec(v) = -v_(0)hat(i)`. Find the instantaneous force `vec(F)` on the particle . Assume that space is gravity free.
(b) If an external uniform magnetic field `B_(0) hat(j) ` is applied , determine the force `vec(F)_(1) and vec(F)_(2)` on the semicircles `KLM and KNM` due to the field and the net force ` vec(F)` on the loop.