A wheel of radius ` R` having charg `Q`, uniformly distributed on the rim of the wheel is free to rotate about a light5 horizontal rod. The rod is suspended by light inextensible strings and a magnetic field `B` is applied as shown in the figure. The initial tensions in the strings are `T_(0)`. If the breaking tension of the strings are `(3T_(0))/(2)`, find the maximum angular velocity `omega_(0)` with which the wheel can be rotated.

Answer

A, B

Explanation

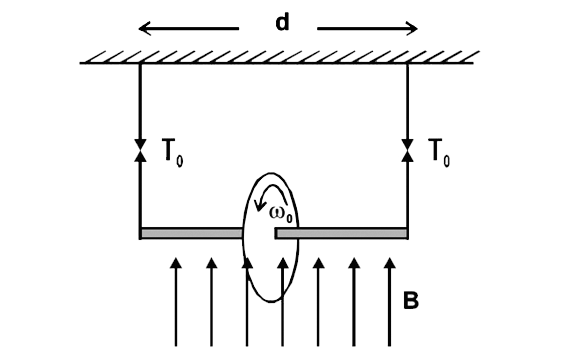
When the ring is not rotating
wt. of ring = Tension in string
`mg = 2 T_(0)`
:. `T_(0) = (mg)/(2)` …..(i)
when the ring is rotating , we can treat it as a current carrying loop . The magnetic moment of this loop
` M = iA = (Q)/(T)xx pir^(2) = (Q)/(2pi) omega xx piR ^(2)`
This current carrying loop will create its own magnetic field which will interact with the given vertical magnetic field in such a way that the tensions in the strings will become unequal. Let the tensions in the strings be `T_(1) + T_(2) = mg` ....(ii)
Torque acting on the ring about the centre of ring
` vec(tau) = vec(M)xxvec(B)`
`tau = M xx B xx sin 90^(@)`
`(Q)/(2 pi) omega xx pi R ^(2) xx B = (QomegaBR^(2))/(2)`