A steady current `I` goes through a wire loop `PQR` having shape of a right angle triangle with `PQ = 3x, PR = 4x and QR = 5x`. If the magnitude of the magnetic field at `P` due to this loop is `k((mu_(0)I)/(48 pi x))`, find the value of `K`.

Explanation

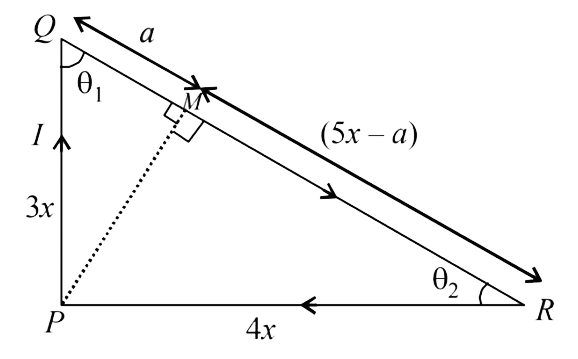
The right angled triangle is shown in the figure . Let us drop a perpendicular from `P` on `QR` which cuts `QR at M`.
The magnetic field due to currents in `PQ and RP` at P` is zero.
The magnetic field due to currents in `QR` at P` is
` B = (mu_(0))/(4 pi) (1)/(PM) (cos theta_(1) + cos theta _(2))` ....(i)
In `Delta PQM`,
`9x^(2) = PM^(2)+a^(2)` ......(ii)
In `DeltaPRM`,
`16x^(2) = PM^(2) + (5x -a)^(2) ....(iii)
rArr ` 7x^(2) = 25x^(2) - 10xa rArr 10xa = 18x^(2)`
rArr `a = 1.8 x` .... (iv)
From (ii) & (iv),
` 9x^(2) = PM^(2) + (1.8x)^(2)`
rArr `PM = sqrt( 9x^(2) -3.24x^(2)) = sqrt(5.76x^(2) = 2.4x` ...(v)
Also ` cos theta_(1) = (a)/( 3x) = (1.8x)/(3x) = 0.6` .....(vi)
` cos theta^(2) = ( 5x -a)/( 4 x) = (5x - 1.8x)/( 4x) = (3.2)/(4) = 0.8` ....(vii)
From (i),(vi) and(vii),
`B = (mu_(0))/(4 pi) xx (I)/( 2.4x) [0.6 + 0.8] = (mu_(0))/( 4 pi) xx(I)/( 2.4 x) xx1.4 = 7 [ (mu_(0)I)/(48 pi x)]`
Comparing it with `B` = k[ (mu_(0)I)/( 48 pi x)]` , we get , ` k = 7`.