A long circular tube of length `10 m` and radius ` 0.3 m` carries a current `I` along its curved surface as shown . A wire - loop of resistance `0.005 ohm` and of radius `0.1 m` is placed inside the tube its axis coinciding with the axis of the tube . The current varies as `I = I_(0)cos(300 t)` where `I_(0)` is constant. If the magnetic moment of the loop is `Nmu_(0)I_(0) sin (300 t)`, then 'N' is

Explanation

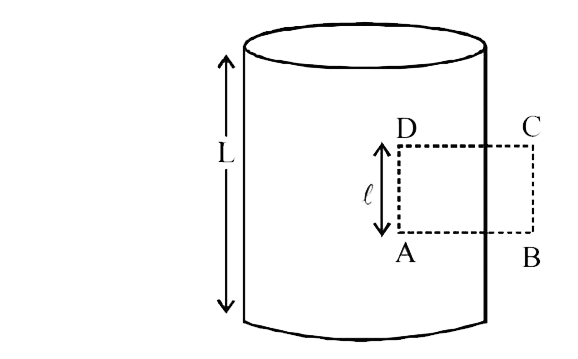
Let us consider an amperian loop `ABCD` which is a rectangle as showm in the figure.
Applying ampere's circuital law we get
`oint vec(B).vec(dl) = mu_(0) xx ( current passing through the loop )`
:. `oint vec(B). Vec(dl) = mu_(0)((I)/(L))xxl`
:. `Bxxl = mu_(0) (I)/(L)xxl`
:. `B = (mu_(0)I)/(L) = (mu_(0))/(L)I_(0) cos(300 t)`
The magnetic moment of the loop
` = (current in the loop)xx pir^(2)`
`=(1)/( R )( -(d phi)/(dt)) xx pir^(2)`
` = -(1)/( R ) [ (d)/( dt) ((B xx pir^(2))] xx pir^(2) = -( pi^(2) r^(4))/( R ) ( dB)/(dt )`
`= [ ( pi^(2) r^(4))/( R ) xx(mu_(0))/(L)I_(0) sin ( 300 t)]xx 300`
Comparing it with the experssion given in the question we get
` N = ( 300 pi^(2)r^(4))/( R )xx(I)/(L) = ( 300(3.14)^(2)xx(0.1)^(4))/(0.005xx10) = 6`