The graph between the stopping potential `(V_(0)) and ((1)/(lambda)) ` is shown in the figure `phi_(1) , phi_(2) and phi_(3)` are work function , which of the following is //are correct

Options

A. ` phi _(1) : phi_(2) : phi_(3) = 1 : 2 : 4`
B. ` phi _(1) : phi_(2) : phi_(3) = 4 : 2 : 1`
C. `tan theta prop (hc)/€`
D. ultravioletight can be used emit photoelectrons from metal `2` and `3 only`

Answer

A, C

Explanation

`phi_(1) : phi_(2) : phi_(3) : = eV_(0_1) : eV_(0_2) : eV_(0_3)`
`V_(0_1) :V_(0_2) :V_(0_3) = 0.001 : 0.002 : 0.004 = 1 : 2 : 4`
therefore option (a) is correct

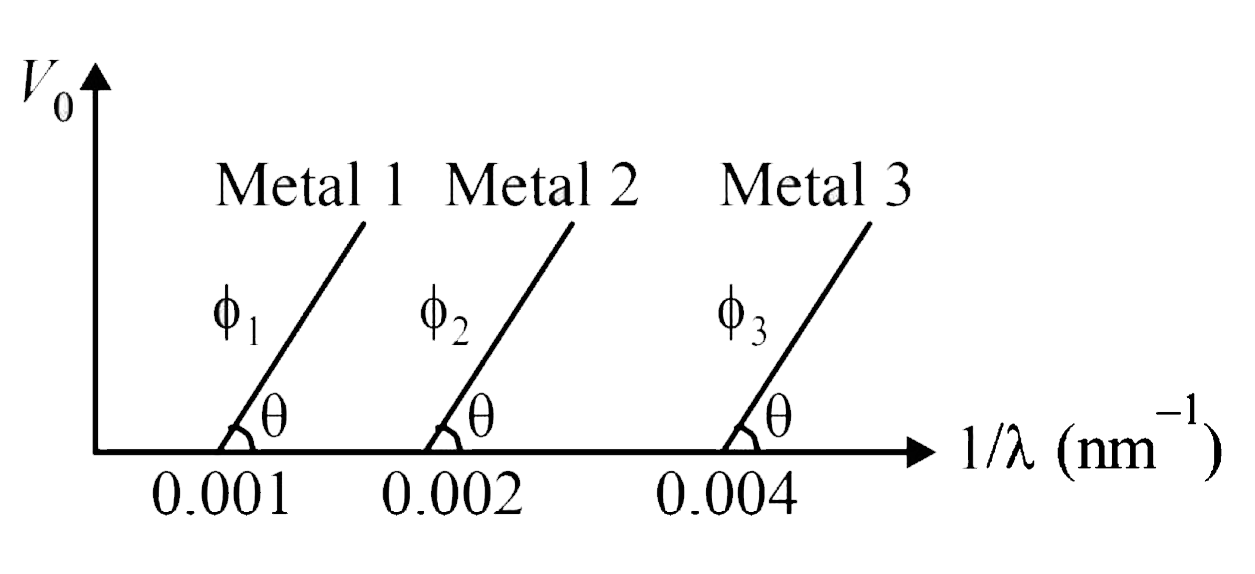
by Einstein's photoelectric equation `(hc)/(lambda) phi = eV`
`rArr V = (hc)/(e lambda) - (phi)/(e) ` ....(i)
comparing equation (i) by `y = mx + c ` , we get the slope of the line `m = (hc)/(e) = ten theta `
`rArr ` option (c ) is currect
from the graph it is clear that
` (1)/(lambda_(0_1) = 0.001 (nm)^(-1) rArr lambda_(0_1) = (*1)/(0.001) = 1000 nm `
also` (1)/(lambda_(0_2)) = 0.002 (nm) ^(-1) rArr lambda_(0_2) = 500 nm`
and ` lambda_(0_3) = 250 nm `