A monochormatic point source radiating wavelength `6000Å` with power `2` vate an aperture A of diameeter `0.1 m` and a lorge screen SC are placed as shown in fig, A photoemissive detector D of surface area `0.5 cm^(2)` is placed at the centre of the screen . The efficiency of the detector for the photoelectron generation per incident photon is `0.9`

(a) Calculate the photon flat at the centre of the screen and the photocurrwect in the detector.
(b) If the concave lens L of focal length `0.6` m is inserted in the aperture as shown . find the new values of photon flot and photocurrect Assume a uniform average transmission of `80%` from the lens .
(c ) If the work function of the photoemissive surface is `1eV` . calculate the values of the stopping potential in the two cases (within and with the lelens in the epertuire).

Answer

A

Explanation

Energy of one photon, `E= (hc)/(lambda) = ((6.6 xx 10^(-34)) (3.0 xx 10^(8))/(6000 xx 10^(-10)) `
`= 3.3 xx 10^(-19) J`

power of the source is `2 W or 2 J//s` therefore number of photons emitted per second
`n_(1) = (2)/(3.3 xx 10^(-19)) = 6.06 xx 10^(18) //s`
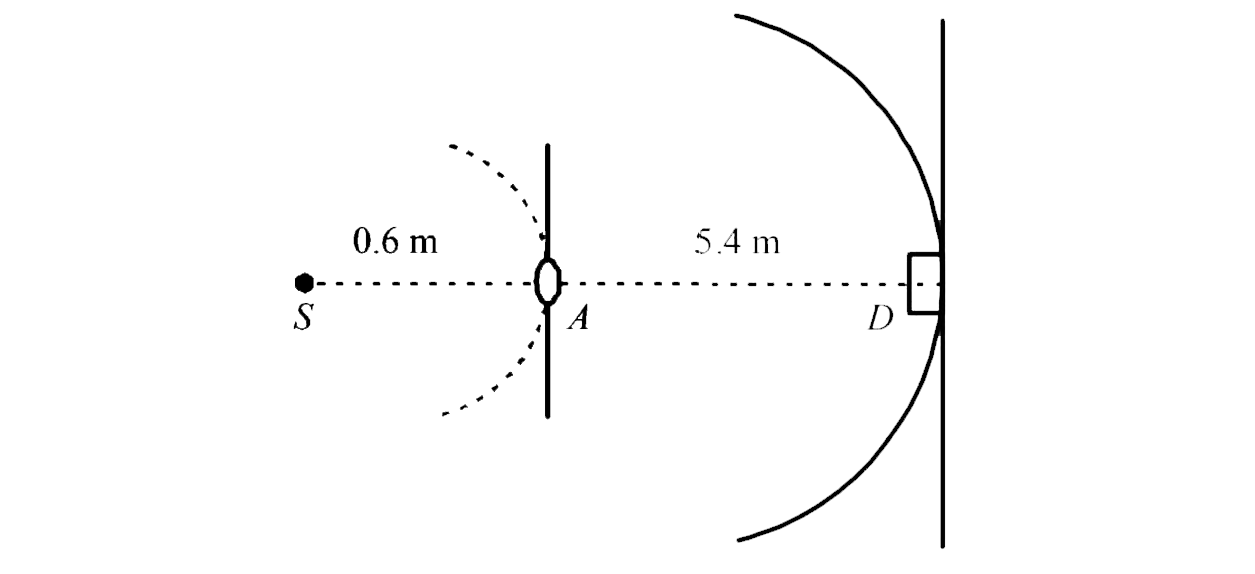
As distance `0.6 m ` number of photon incident per area per unit time
`n_(2) = (n_(1))/(4 pi (0.6)^(2)) = 1.34 xx 10^(18) //m^(2) //s`
Area of aperture is ,
`S_(1) = (pi)/(4)d^(2) = (pi)/(4) (0.1)^(2) = 7.85 xx 10^(-3)m^(2)`
`:.` Total number of photons incident per unit time on the aperture
`n_(3) = n_(2) s_(1)= (1.34 xx 10^(18) ) (7.85 xx 10^(-3)) //s`
The aperture will because new source of light
Now these photon are further distributed is all directions
Heance at thr location of detector, photons incident per unit area per unit time
`n_(4) = (n_(3))/(4 pi (6.0)^(2)) = (1.052 xx 10^(16))/(4 pi (5.4)^(2)) `
`= 2.87 xx 10^(13 )s^(-1) m^(-2)`
This is the photon this at the centre of the Area of detector is `0.5 cm^(2) or 0.5 xx 10^(-4)m^(2)` therefore , total number of photonelectrons gmerated per unit time
`n_(6) = 0.9n_(2) = 1.2915 xx 10^(8)s^(-1)`
or, photocurrect in the detectir
`i = (e) n_(6) = (1.6 xx 10^(-19)) (1.2915 xx 10^(9)) = 2.07 xx 10^(-10)A`
(b) using the lens formula
`(1)/(v) - (1)/(-0.6) = (1)/(-0.6) or v = - 0.33 m`
i,e, image of souece (say S, is formed at `0.3m ` from the lens)
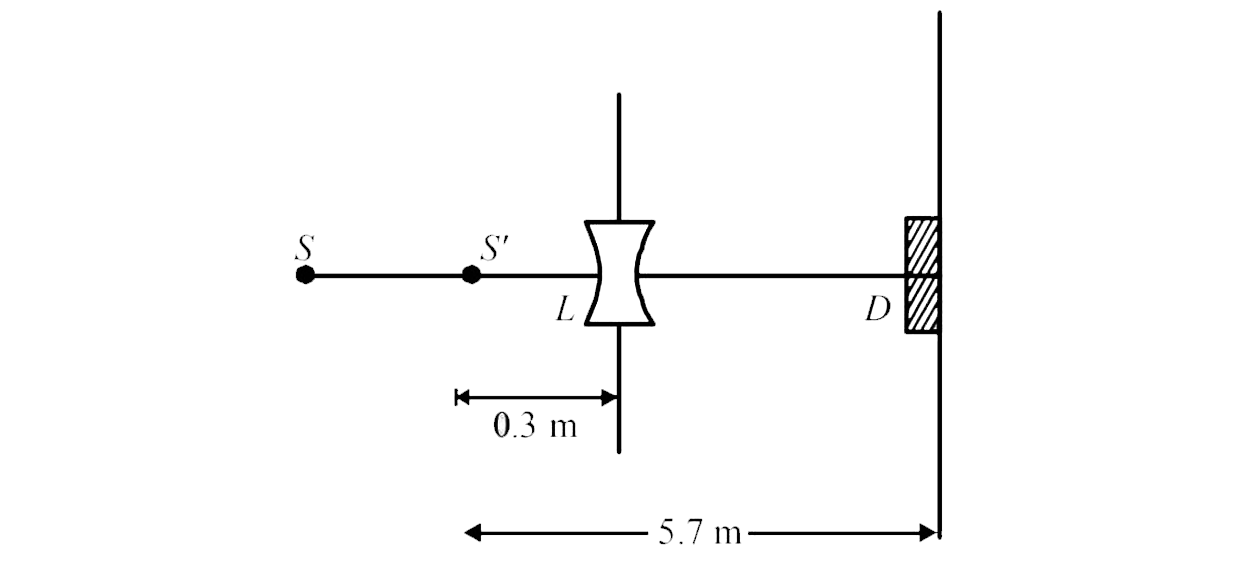
Total number of incident per unit on the lens are still `n_(2) or 1.052 xx 10^(16) //s` of it transmits to secound medum .Therefore , at a distance of `5.7`m from `S` number of be photon incident per unit time will be
`n_(7) = ((80 //100) (1.05 xx 10^(16)))/((4 pi)(5.7)^(2)) = 2.06 xx 10^(13) s^(-1) m^(-2)`
for stopping potential
`(hc)/(lambda) = (E_(lambda)) _(max) + W = eV_(0) + W`
`:. eV_(0) = (hc)/(lambda) - W = (3.315 xx 10^(-19))/(1.6 xx 10^(-19)) - 1 = 1.07 Volt`