To determine the half life of a radioactive element , a student plot a graph of in `|(dN(t))/(dt)|` versus `t` , Here `|(dN(t))/(dt)|` is the rate of radiation decay at time t , if the number of radioactive nuclei of this element decreases by a factor of p after `4.16 `year the value of p is

Explanation

we know that `N = N_(0)e^(-lambda t)`
:. (dN)/(dt) = N_(0)e^(-u) (-lambda) = -N_(0)e^(-11)`
Taking log on both sides
`(dN)/(dt) = log_(e) (-N_(0) lambda)) - lambda t `
Comparting it with the graph line
we get `lambda= (1)/(2)gamma t^(-1) [(AC)/(BC) = (1)/(2))]`

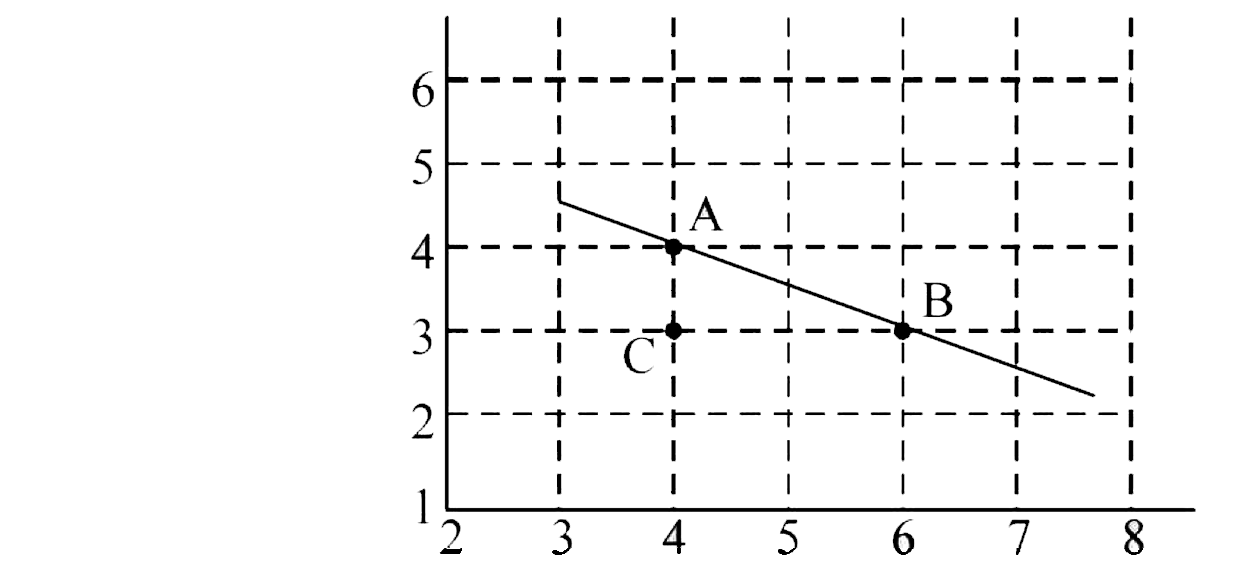
`:. T_(1//2) = ((0.693)/(lambda) = 0.693 xx 2 = 1.386 year`
Now` (N)/(N_(0)) = ((1)/(2))^(1)/(T_(1//2)) rArr (1)/(p)= ((1)/(2)) ^(4.13)/*(1.386)) = (1)/(8)`