Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERS- MARCH 2018-SECTION - II
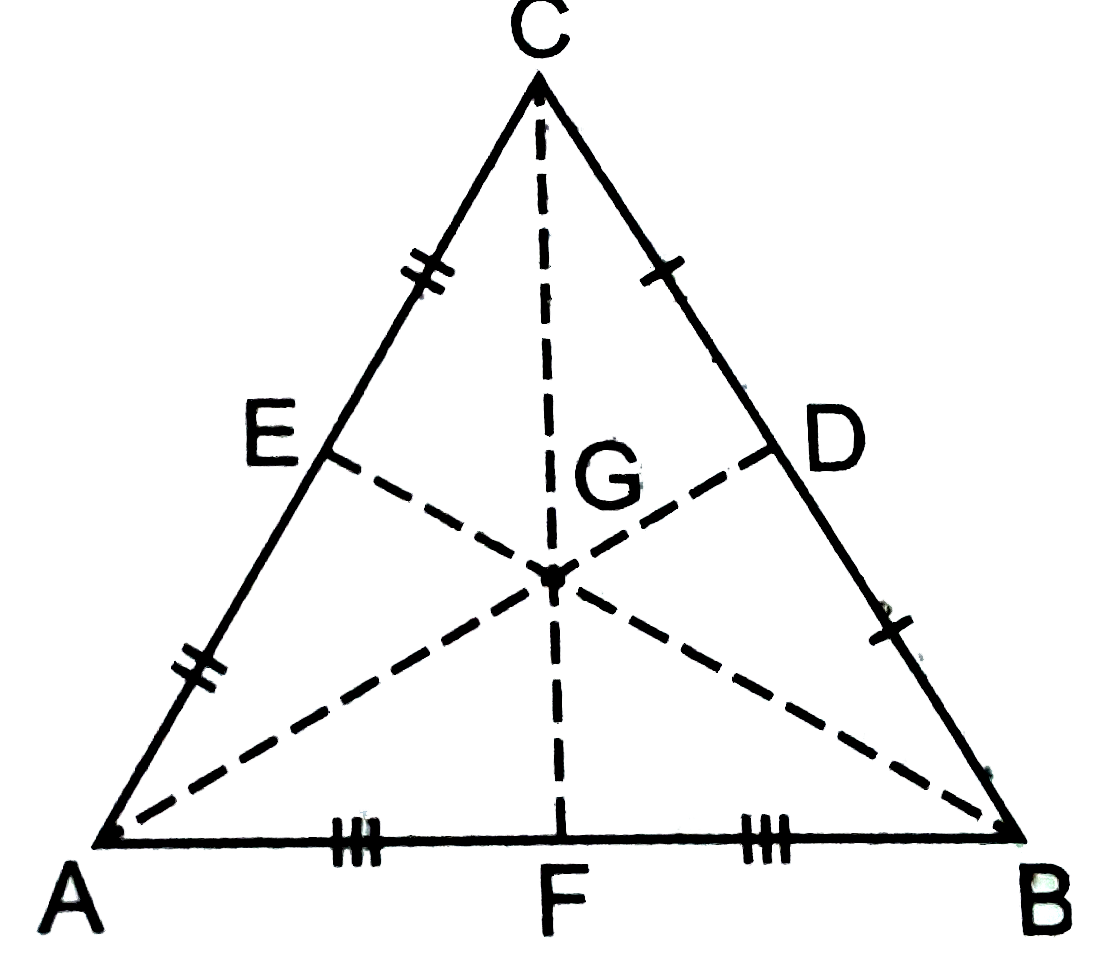
- Prove using vectors: Medians of a triangle are concurrent.
Text Solution
|
- Let the p.m.f. of a random variable X be - P(x) = (3 -x)/10 " for ...
Text Solution
|
- if int0^k (dx)/(2+8x^2)=pi/16 then find the value of k
Text Solution
|
- Integrating factor of linear differential equation x(dy)/(dx) + 2y = ...
Text Solution
|
- Evaluate : int e^(x) [(cos x - sin x)/(sin^(2) x)] dx.
Text Solution
|
- if y = tan^(2) (log x^(3))," find " (dy)/(dx).
Text Solution
|
- Find the area of ellipse x^(2)/1 + y^(2)/4 = 1.
Text Solution
|
- Obtain the differential equation by eliminating the arbitrary constant...
Text Solution
|
- Given X~ B (n,P) If n= 10 and p=0.4 , find E(X) and Var (X) .
Text Solution
|
- Evaluate : int 1/(3+2 sin x + cos x) dx.
Text Solution
|
- If x=acos^(3)t,y=asin^(3)t,"show that "(dy)/(dx)=-((y)/(x))^((1)/(3))
Text Solution
|
- Examine the contionuity of the following functions at the give points ...
Text Solution
|
- Find all the points of local maxima and minima and the correspondin...
Text Solution
|
- Prove that : int 1/(a^(2)-x^(2)) dx = 1/(2a) log |(a+x)/(a-x)|+c.
Text Solution
|
- int(-a)^(a)f(x)dx= 2int(0)^(a)f(x)dx, if f is an even function 0, if...
Text Solution
|
- If f(x)(x^(2)-9)/(x-3)+alpha, "for" x gt 3 =5, "for" x =3 =2x^(2)+...
Text Solution
|
- tan^(-1)((5x+1)/(3-x-6x^(2)))
Text Solution
|
- A fair coin is tossed 8 times. Find the probability that it shows head...
Text Solution
|
- Verify Rolle's theorem for the following function :f(x)=x^2-4x+10 on [...
Text Solution
|
- Find the particular solutions of the following differential equation :...
Text Solution
|
- Find the variance and standard deviation of the random variable X wh...
Text Solution
|