A particle is moving in x-y plane. Its initial velocity and acceleration are `u=(4 hati+8 hatj) m//s and a=(2 hati-4 hatj) m//s^2.` Find
(a) the time when the particle will cross the x-axis.
(b) x-coordinate of particle at this instant.
(c) velocity of the particle at this instant.
Initial coordinates of particle are `(4m,10m).`

Answer

B, D

Explanation

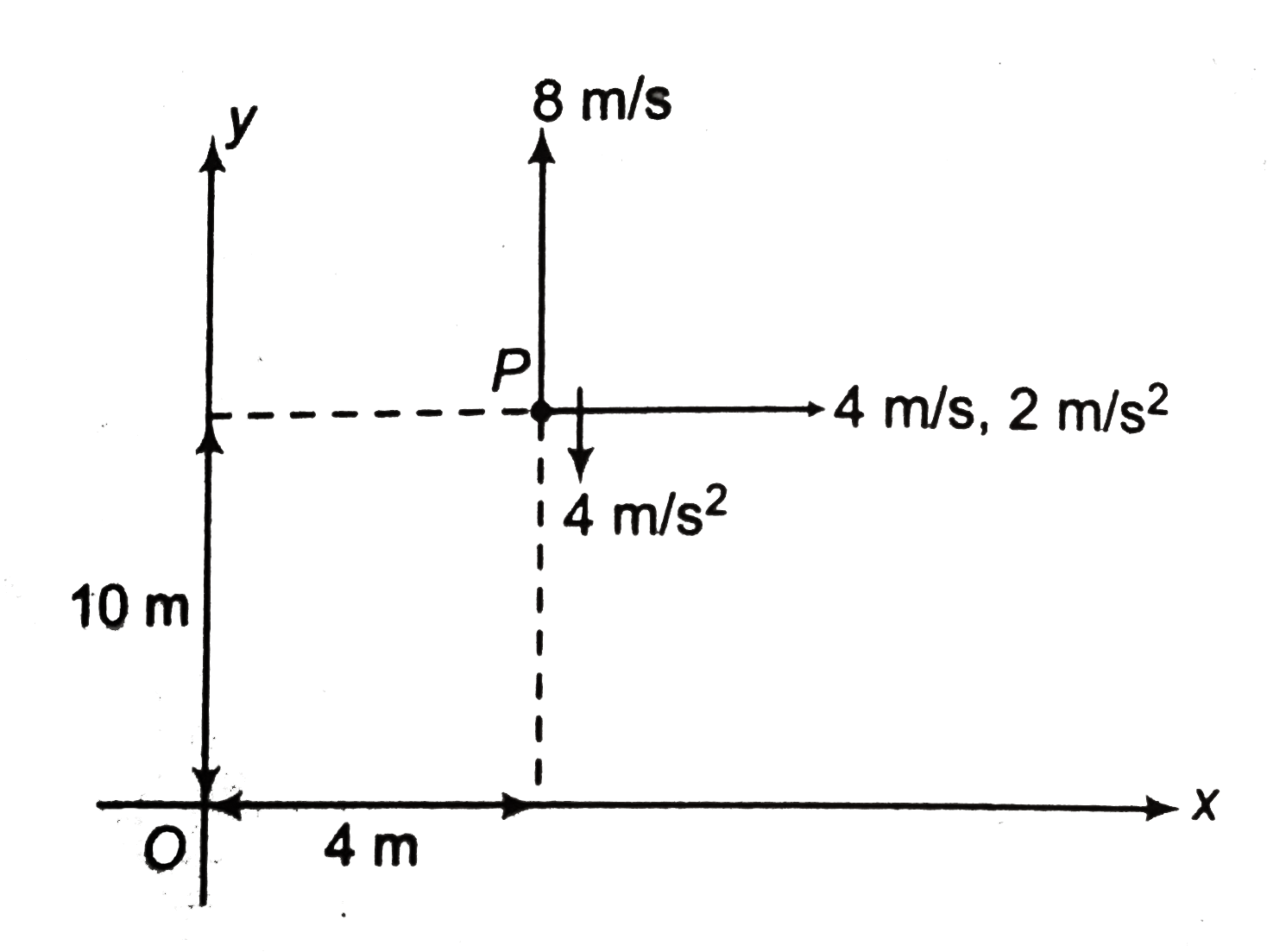
Particle starts from point P. Components of its initial velocity and acceleration are as shown in
figure.
(a) At the time of crossing the x-axis, its y-coordinate should be zero or its y-displacement
(w.r.t initial point P) is `-10m.`
Using the equation, `s_y=u_yt+1/2 a_yt^2 `
`-10=8t-1/2xx4xxt^2`
Solving this equation, we get positive value of time,
`t=5s`
(b) x-coordinate of particle at time t:
x=initial x-coordinate +displacement along x-axis or `x=x_i+s_x` (at time t)
`=x_i+u_xt+1/2 a_x t^2`
Substuting the proper values, we have,
`x=4+(4xx5)+1/2xx2xx(5)^2=49 m`
(c) Since, given acceleration is constant, so we can use,
`v=u+at`
`:. v=(4 hati+8 hatj)+(2 hati-4 hatj)(5)`
`=(14 hati-12 hatj) m//s`