Home
Class 11
PHYSICS
Two uneqal masses of 1 kg and 2 kg are a...

Two uneqal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown . If the system is released from rest, find the work done by string on both the blocks in 1 s.
(Take `g= 10 m//s^2`).

Text Solution

Verified by Experts

The correct Answer is:
B
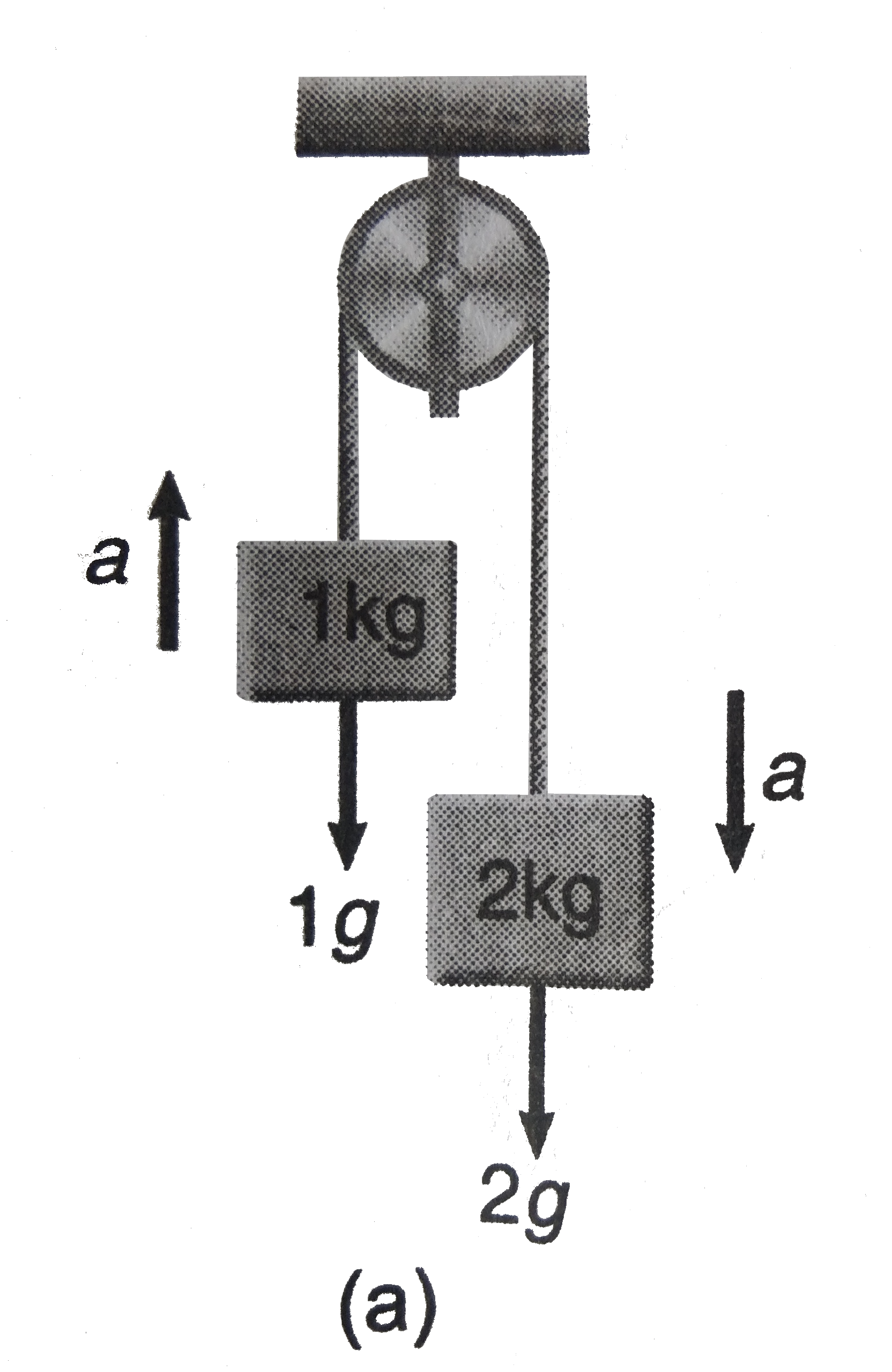
Net pulling for on the system is
`F_("net")=2g-lg=20-10=N`
Toal mass being pulled `m=(+2)=3kg`
Therfore, acceleration of the system will be
`a=(F_("net"))/(m)=(10)/(3)m//s^2`
Displacement of both the blocks in `1 s` is
`S=1/2at^2=1/2((10)/(1))(1)^2=(5)/(3)m `
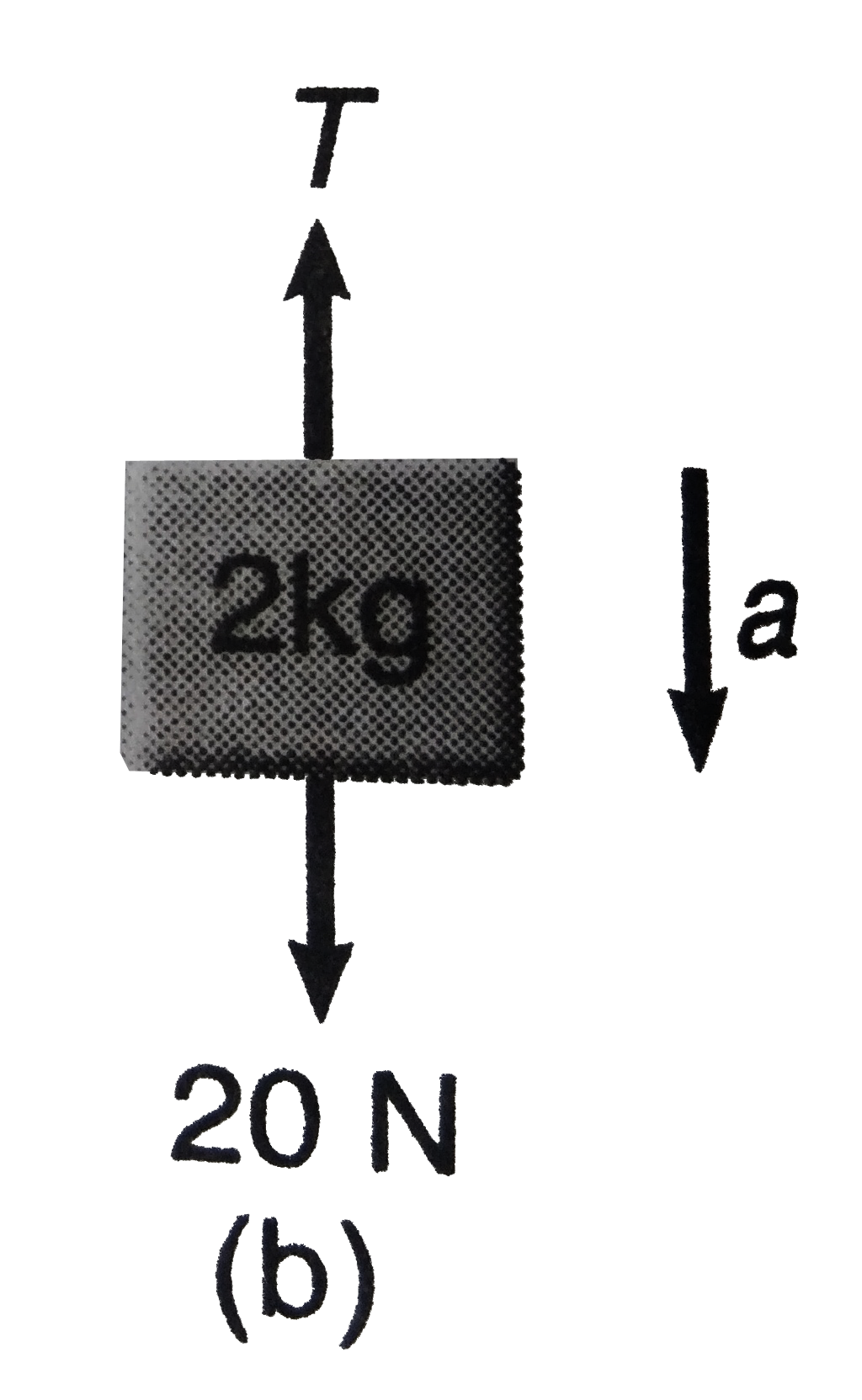
Free bosy diagram of 2 kg block is shown.(b).
Using `sumF=ma,` we get
`20-T=2_a=2(10/3)` or `T=20-20/3=40/3N`
`:.` work done by sting (tension) on `1 kg` block in `1 s` is
`W_2=(T)(S)cos 0^@)`
=`(40/3)(5/3)(1)=200/9J`
similarly, work done by string on 2 kg block in 1 s will be
`W_2=(T)(S)(cos 180^@)`
`=(40/3)(5/3)(1)=200/9J`.

Promotional Banner

Topper's Solved these Questions

  • WORK, ENERGY & POWER

    DC PANDEY|Exercise Solved Examples|12 Videos

  • WORK, ENERGY & POWER

    DC PANDEY|Exercise TYPE2|1 Videos

  • WAVE MOTION

    DC PANDEY|Exercise Integer Type Question|11 Videos

  • WORK, ENERGY AND POWER

    DC PANDEY|Exercise MEDICAL ENTRACES GALLERY|33 Videos

Similar Questions

Explore conceptually related problems

Two unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown in figure. If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g = 10 ms^(-2) )

Two masses of 10 kg and 6 kg connected at the two ends of an inextensible string pass over a smooth frictionless pulley . Calculate acceleration of the system and tension in the string .

Two blocks of masses 6 kg and 4 kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be

Two masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .

Two masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.

Two masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :

Two unequal masses of 1kg and 2kg are connected by an inextensible light string passing over a smooth pulley as shown in figure. A force F = 20N is applied on 1kg block find the acceleration of either block (g = 10m//s^(2)) .

Two masses M_(1)=5kg,M_(2)=10 kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be