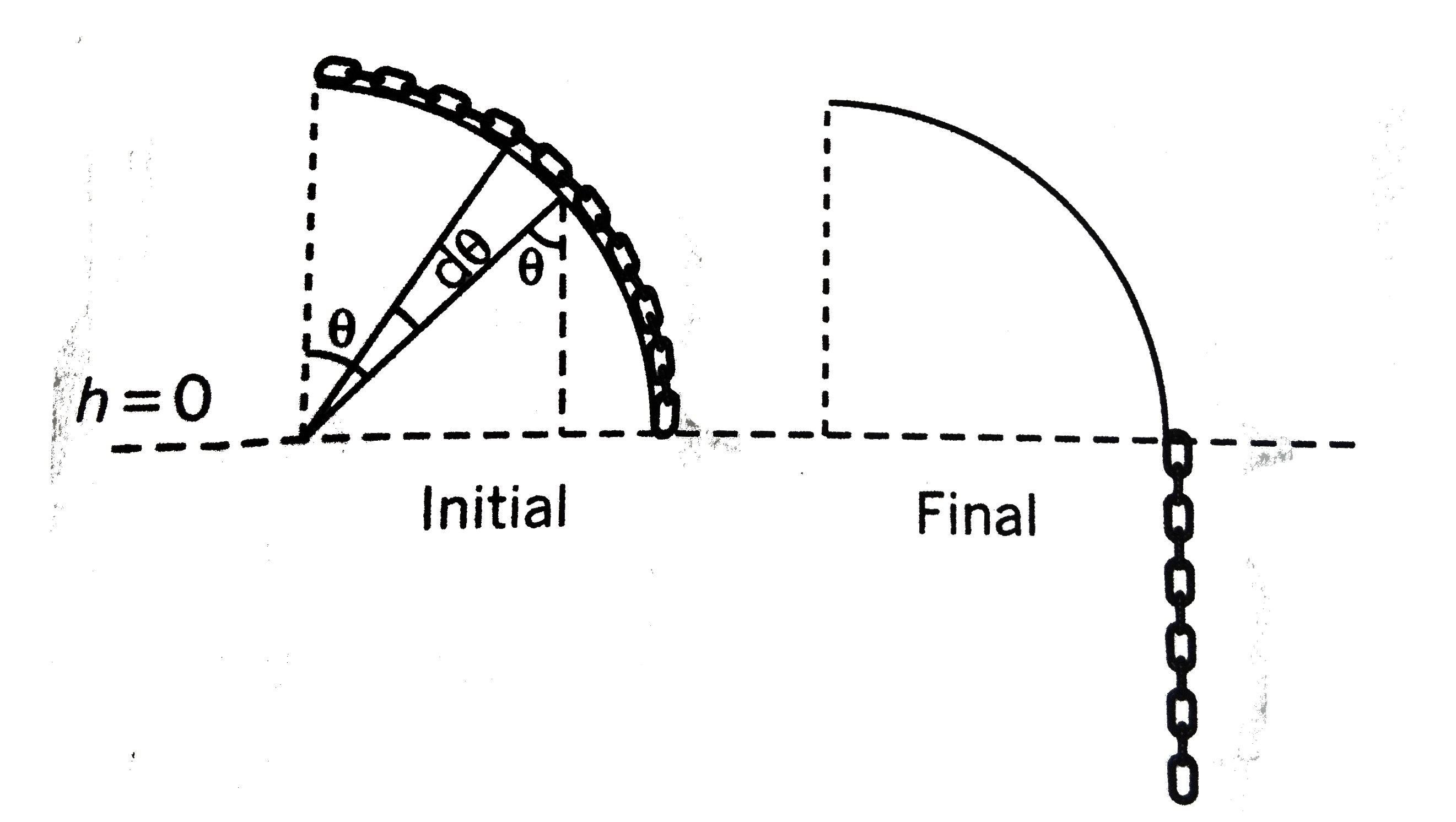Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY-WORK, ENERGY & POWER-Level 2 Subjective
- Two block of masses m(1) and m(2) connected by a light spring rest on ...
Text Solution
|
- The flexible bicycle type chain of length (pir)/2 and mass per unit le...
Text Solution
|
- A baseball having a mass of 0.4 kg is thrown such that the force actin...
Text Solution
|
- A chain (AB) of length l loaded in a smooth horizontal table so that i...
Text Solution
|
- The block shown in the figure is acted on by a sping with spring const...
Text Solution
|
- A spring mass system is held at rest with the spring relaxed at a heig...
Text Solution
|
- A block of mass m moving at a speed v compresses a spring throgh a dis...
Text Solution
|
- In the figure shown masses of the blocks A, B and C are 6kg, 2kg and 1...
Text Solution
|
- A body of mass m slides down a plane inclined at an angle alpha. The c...
Text Solution
|
- A particle moving in a straight line is acted upon by a force which wo...
Text Solution
|
- AS chain of length l and mass m lies o the surface of a smooth sphere ...
Text Solution
|
- Find the speed of both the blocks at the moment the block m(2) hits th...
Text Solution
|
- A block of mass M slides along a horizontal table with speed v(0). At ...
Text Solution
|
- A small block of ice with mass 0.120 kg is placed against a horizontal...
Text Solution
|
- A 0.500 kg block is attached to a spring with length 0.60m and force c...
Text Solution
|
 .
.