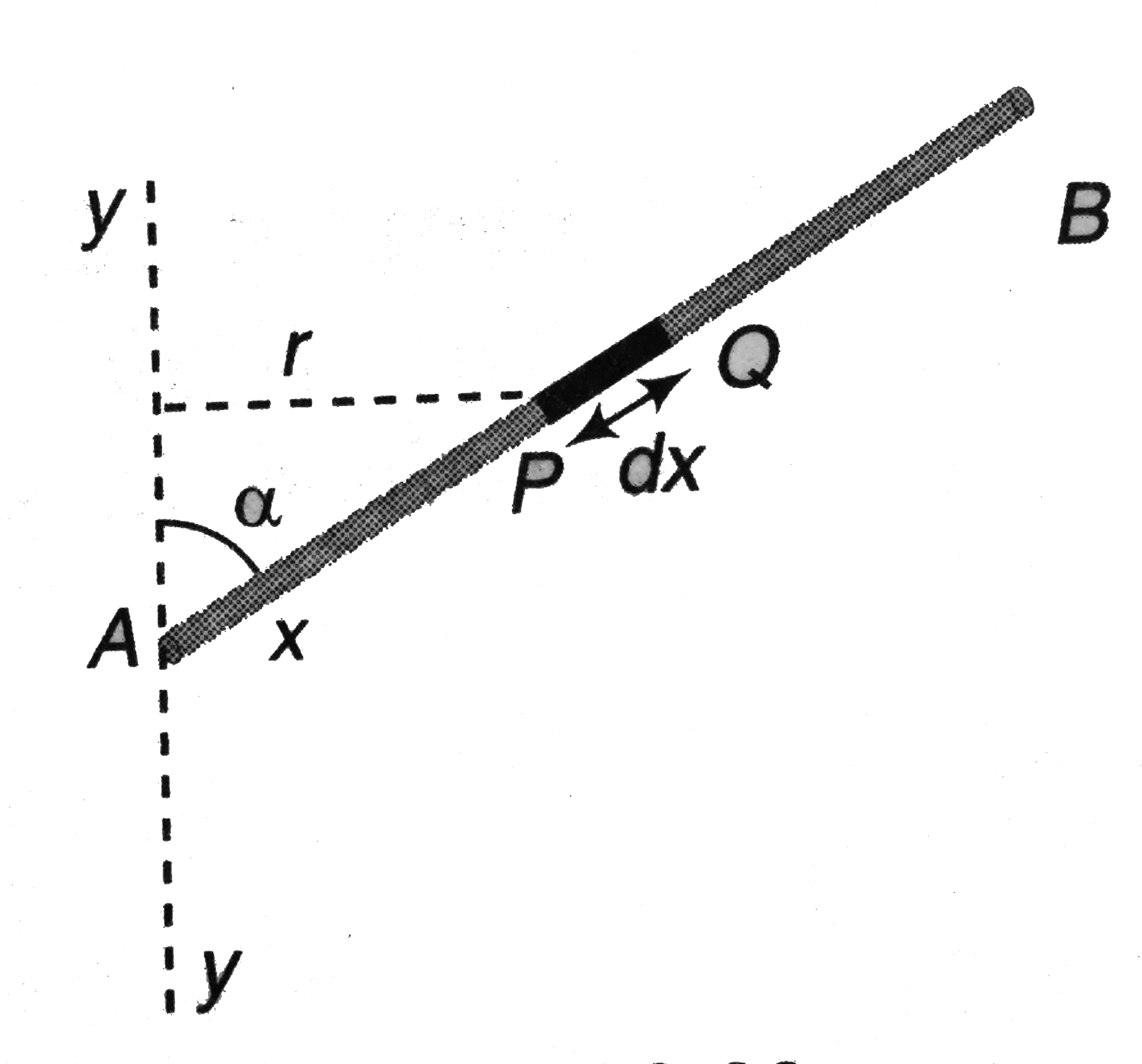
Mass per unit length of the rod `=(m)/(l)`
Mass of an element `PQ` of the rod is `dm=((m)/(l))dx`
jPerpendicular distance of this elemental mass about yy is `r=xsinalpha`
`therefore` moment of inertia of this small element of the rod (can be assumed as a point mass) about yy is
`dI=(dm)r^(2)=((m)/(l)dx)(xsinalpha)^(2)=((m)/(l)sin^(2)alpha)x^(2)dx`
`therefore` moment of inertial of the complete rod,
`I=int_(x=0)^(x=l)dI=(m)/(l)sin^(2)alphaint_(0)^(l)x^(2)dx=(ml^(2))/(3)sin^(2)alpha`