Rod AB has length L. velocity of end A of the rod has velocity `upsilon_(0)` at the given instant.
(a). Which type of motion the rod has?
(b). Find velocity of end B at the given instant.
(C). Find the angular velocity of the rod.

Explanation

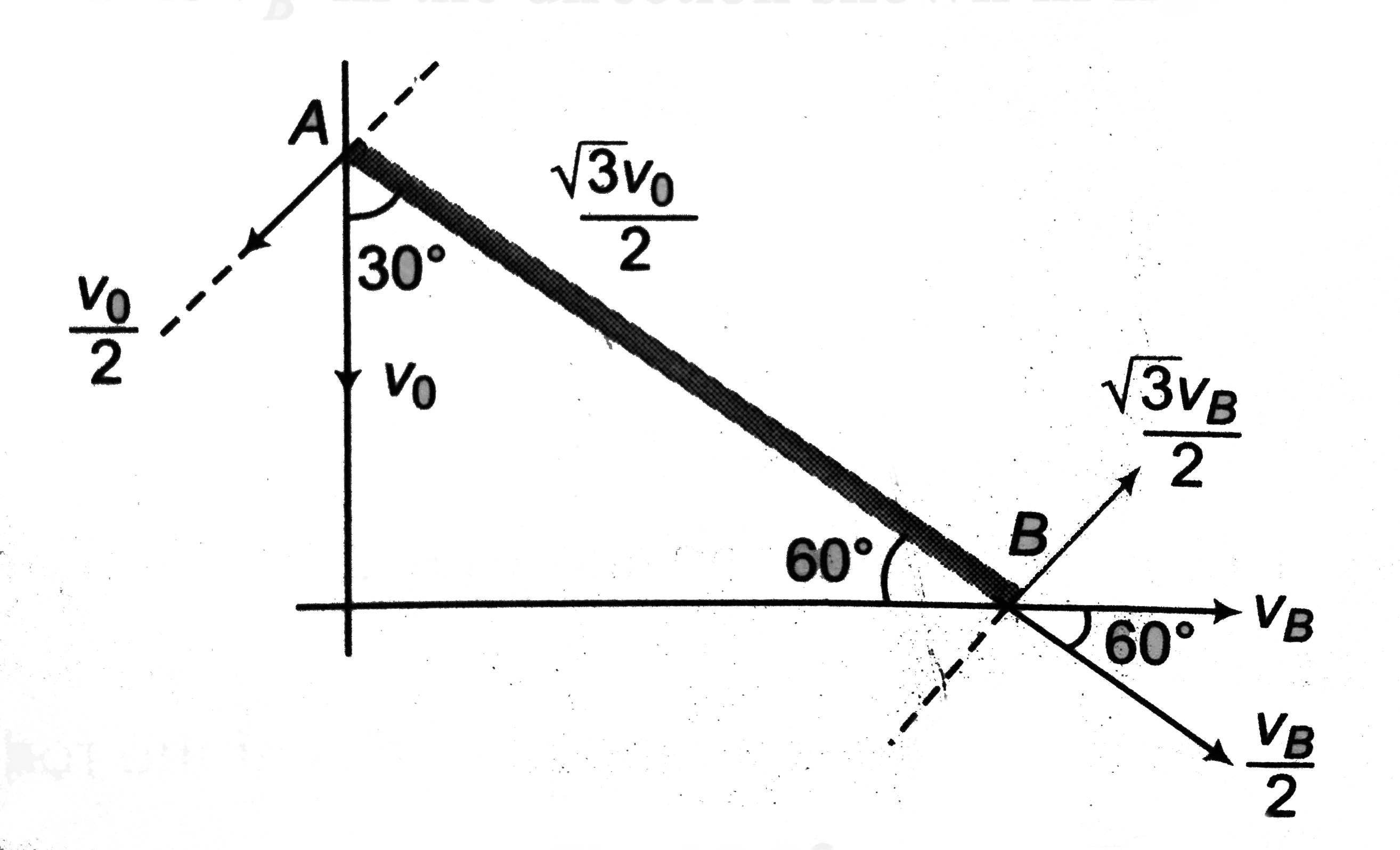
(a). The rod has rotational plus translational motion.
(b). Let velocity of end B is `V_(B)` is the direction shown in figure.
Components of `V_(A)` and `V_(B)` along AB and perpendicular to AB are also shown in the same figure.
Rod is a rigid body. so, distance AB should remain constant or the components along AB should be same.
(c).
Perpendicular to AB, components will be
`v_(r)=(v_(0))/(2)+(sqrt(3)v_(B))/(2)`
substituting `v_(B)=sqrt(3)v_(0)` we get `v_(r)=2v_(0)`
Now angular velocity of the rod is `omega=(v_(r))/(AB)`
or `omega=(2v_(o))/(L)`
Rotation of the rod is anticlockwise. Therefore, from right hand rule `omega` is perpendicular to paper outwards or in `odot` direction.