Home
Class 11
PHYSICS
In the shown figure, a=2m//s^(2),omega...


In the shown figure,
`a=2m//s^(2),omega=(2t)rods^(-1)` and `CP=1m`
In terms of `hati` and `hatj`, find linear acceleration of the particle at `P` at `P` at `t=1` s

Text Solution

Verified by Experts

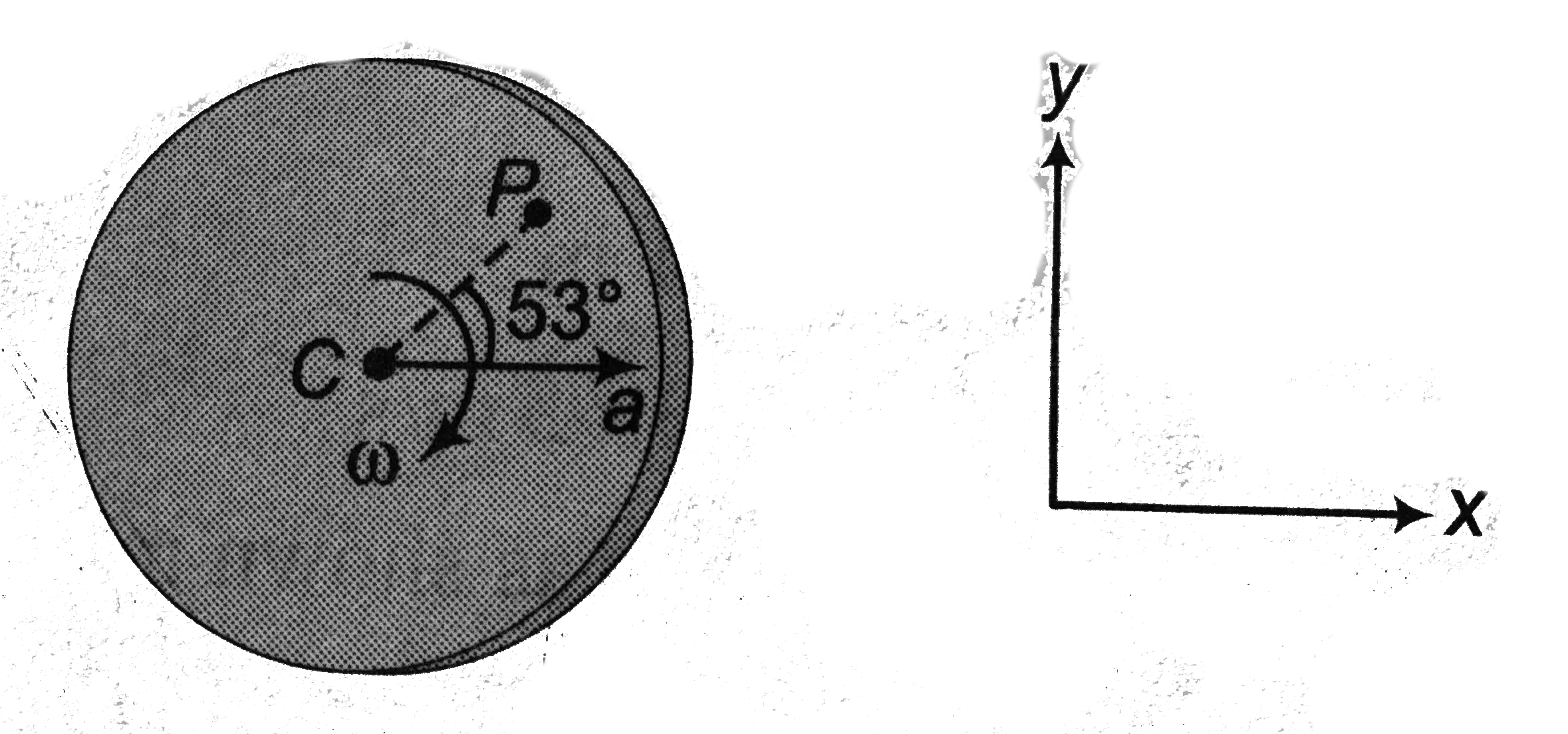
For particle at `P`
`r=CP=1m`
`impliesalpha=(domega)/(dt)=(d)/(dt)(2t)=2rad//s^(2)`
At `t=1` s
`omega=2rad//s`
`alpha=2rad//s^(2)`
`a_(t)=ralpha=2m//s^(2)`
`a_(r)=romega^(2)=4m//s^(2)`
and `a=2m//s^(2)`
Net acceleration of `P` is the vector sum of three terms a, `a_(r)` and `a_(t)` as shown in figure below.
`thereforea_(P)=2hati+(2cos37^(@)hati-2sin37^(@)hatj)+(-4sin37^(@)hati-2sin37^(@)hatj)-(-4sin37^(@)hati-4cos37^(@)hatj)`
`=2hati+1.6hati-1.2hatj-2.4hati-3.2hatj`
`=(1.2hati-4.4hatj)m//s^(2)`
Promotional Banner

Topper's Solved these Questions

  • ROTATIONAL MECHANICS

    DC PANDEY|Exercise Solved Examples|25 Videos

  • ROTATIONAL MECHANICS

    DC PANDEY|Exercise Miscellaneous Examples|2 Videos

  • ROTATION

    DC PANDEY|Exercise (C) Chapter Exercises|39 Videos

  • ROTATIONAL MOTION

    DC PANDEY|Exercise Integer Type Questions|17 Videos

Similar Questions

Explore conceptually related problems

In the figure shown upsilon=2m//s omega=5rad//s and CP=1m In terms of hati and hatj find linear velocity of particle P.

In the figure shown omega=(v)/(2R) in terms of hati and hatj find linear velocities of particles M, N, R and S.

If velcotiy of a particle is given by v=2t-1 then find the acceleration of particle at t = 2s.

A circular disc is rotating with an angular speed (in radian per sec) omega=2t^(2) given, CP=2m In terms of hati,hatj and hatk at t=1s find, (a). omega (b). alpha (c). linear velocity of the particle lying at P (d). linear acceleration of the particle lying P

the angular velocity omega of a particle varies with time t as omega = 5t^2 + 25 rad/s . the angular acceleration of the particle at t=1 s is

In the figure shown, find acceleration of the system and tenslons T_(1),T_(2) and T_(3) (Take = 10 m//s^(2))

Velocity of a particle in x-y plane at any time t is v=(2t hati+3t^2 hatj) m//s At t=0, particle starts from the co-ordinates (2m,4m). Find (a) acceleration of the particle at t=1s. (b) position vector and co-ordinates of the particle at t=2s.

In the sae figure. If v and omega both are constant, then find linear acceleration of point M,N,R and S in terms of R,omega,hati and hatj where R is the radius disc.

If the velocity of a particle is (10+2t^(2)m/s ,then the average acceleration of the particle between 2s and 5s is (in m/s^2)

. If the velocity of a particle is (10 + 2 t 2) m/s , then the average acceleration of the particle between 2s and 5s is