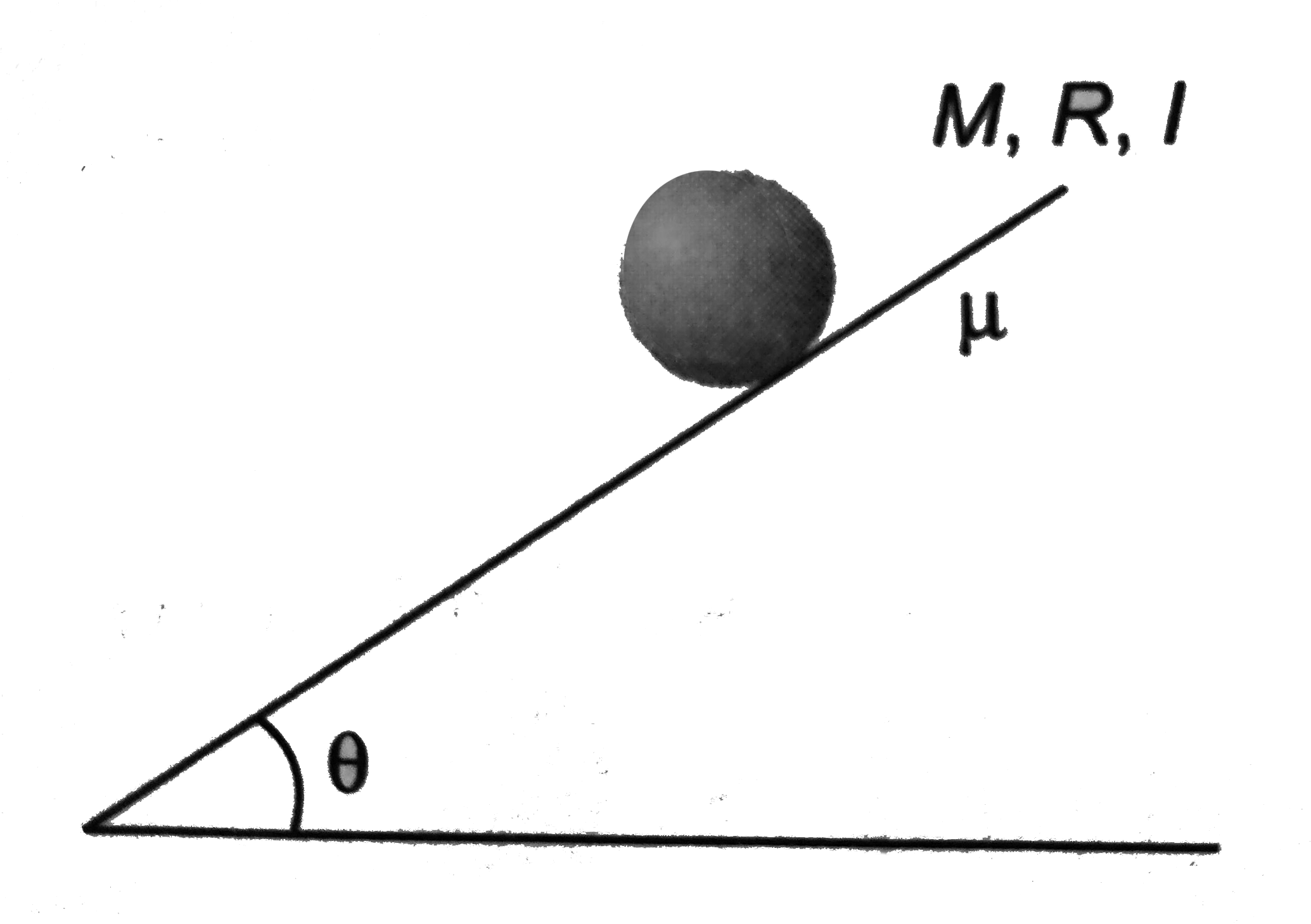
In the shown figure, `M` is mass of the body, `R` its radius an `I` the moment of inertial about an axis passing through centre. Find force of friction `f` acting on the body (upwards), its linear acceleration `a` (down the plane) and type of motion if:
(a) `mu=0`
(b). `multmu_(min)`
(c). `mugtmu_(min)`
Where `mu_(min)` is the minimum value of coefficient of friction required for pure rolling