A tangential force `F` acts at the top of a thin spherical shell of mass `m` and radius `R`. Find the acceleration of the shell if it rolls without slipping.

Explanation

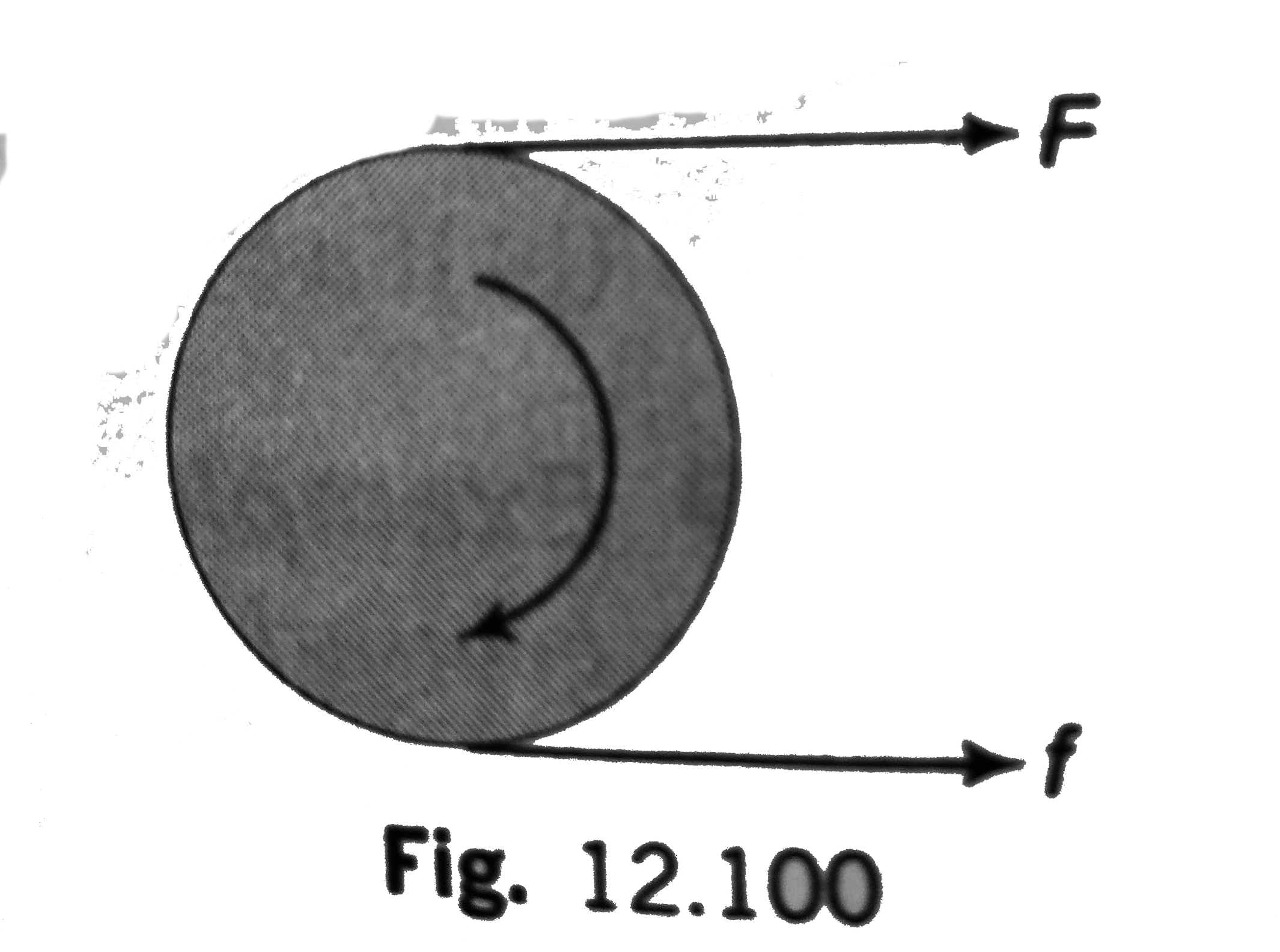
Let `f` be the force of friction between the shell and the horizontal surface.
Force translational motion
`F=f=ma` ..(i)
For translational motion,
`FR-fR=Ialpha=I(a)/(R)`
`[because a=Ralpha` for pure rolling]
Adding eqs. (i) and (ii) we get
`2F=(m+(I)/(R^(2)))a`
`=(m+(2)/(3)m)a=(5)/(3)ma`
or `F=(5)/(6)ma` `[becauseI_("shell")=(2)/(3)mR^(2)]`
`impliesa=(6F)/(5m)`