Home
Class 11
PHYSICS
A solid sphere is rolling without slippi...


A solid sphere is rolling without slipping as shown in figure. Prove that
`(1)/(2)mv^(2)+(1)/(2)l_(C)omega^(2)=(1)/(2)l_(0)omega^(2)`

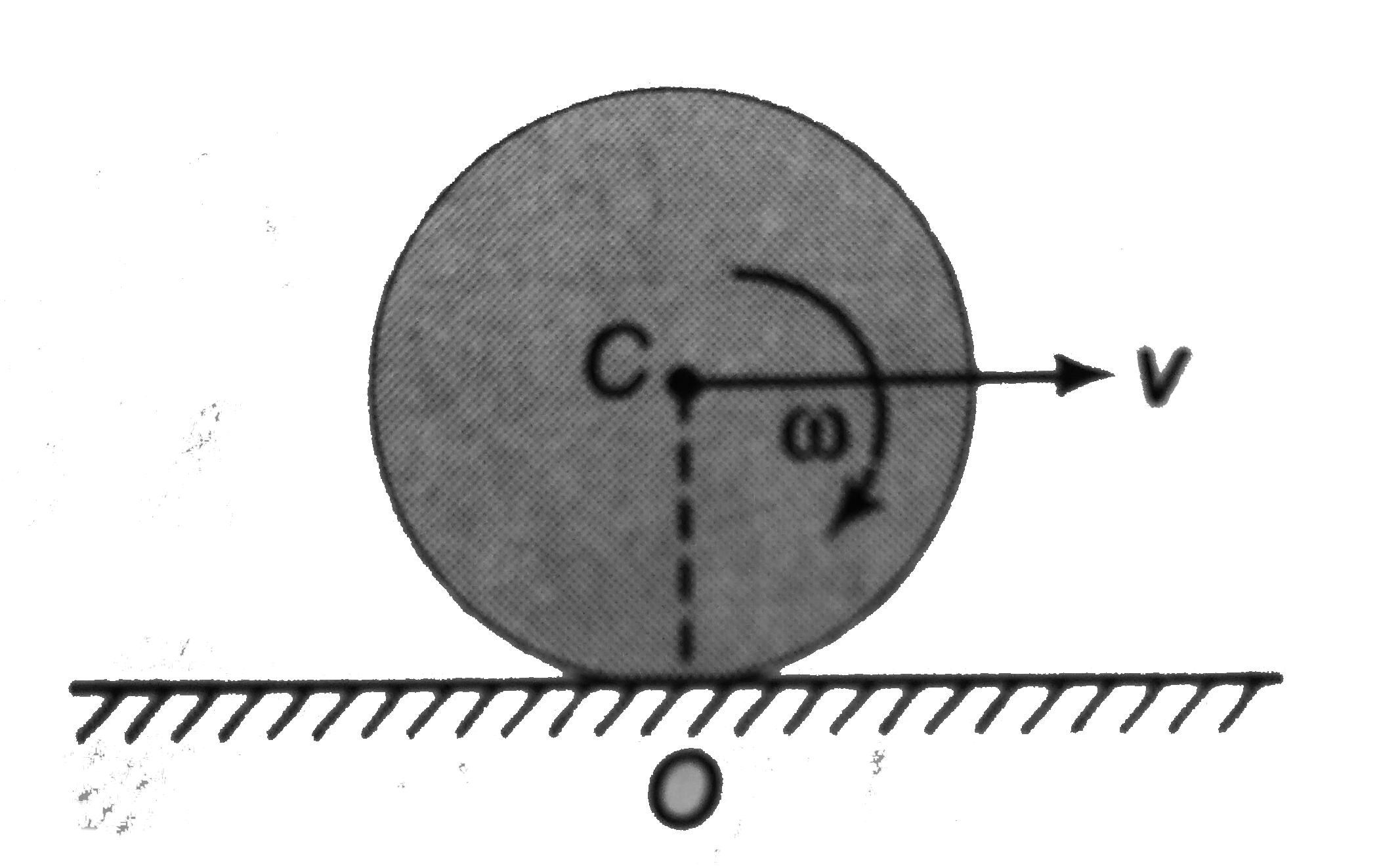
Text Solution

Verified by Experts

`I_(C)=(2)/(5)mR^(2),I_(0)=(7)/(5)mR^(2)` and `omega=(v)/(R)`
substituting these values in the given equation we get the result.
Promotional Banner

Topper's Solved these Questions

  • ROTATIONAL MECHANICS

    DC PANDEY|Exercise Exercise 12.10|5 Videos

  • ROTATIONAL MECHANICS

    DC PANDEY|Exercise Exercise 12.11|2 Videos

  • ROTATIONAL MECHANICS

    DC PANDEY|Exercise Exercise 12.8|3 Videos

  • ROTATION

    DC PANDEY|Exercise (C) Chapter Exercises|39 Videos

  • ROTATIONAL MOTION

    DC PANDEY|Exercise Integer Type Questions|17 Videos

Similar Questions

Explore conceptually related problems

(1)/(2+omega)+(1)/(1+2 omega)=(1)/(1+omega)

(1)/(2+omega)+(1)/(1+2 omega)=(1)/(1+omega)

(1)/(1+2 omega)+(1)/(2+omega)-(1)/(1+omega)=0

Prove that (1-omega-omega^(2))(1-omega+omega^(2))(1+omega-omega^(2))=8

Prove that (1-w+w^2)^5+(1+w-w^2)^5=32

A 1 Kg solid sphere rolls without slipping on a rough horizontal suface as shown in figure. Select incorrect alternative

Prove that, (1-w+w^2)^4+(1+w-w^2)^4=-16

Prove that omega(1+omega-omega^(2))=-2

If omega_(1) is complex cube root of that (1)/(a+omega)+(1)/(b+omega)+(1)/(c+omega)=2 omega^(2) and (1)/(a+omega^(2))+(1)/(b+omega^(2))+(1)/(c+omega^(2))=2 omega then the value of (1)/(a+1)+(1)/(b+1)+(1)/(c+1)=