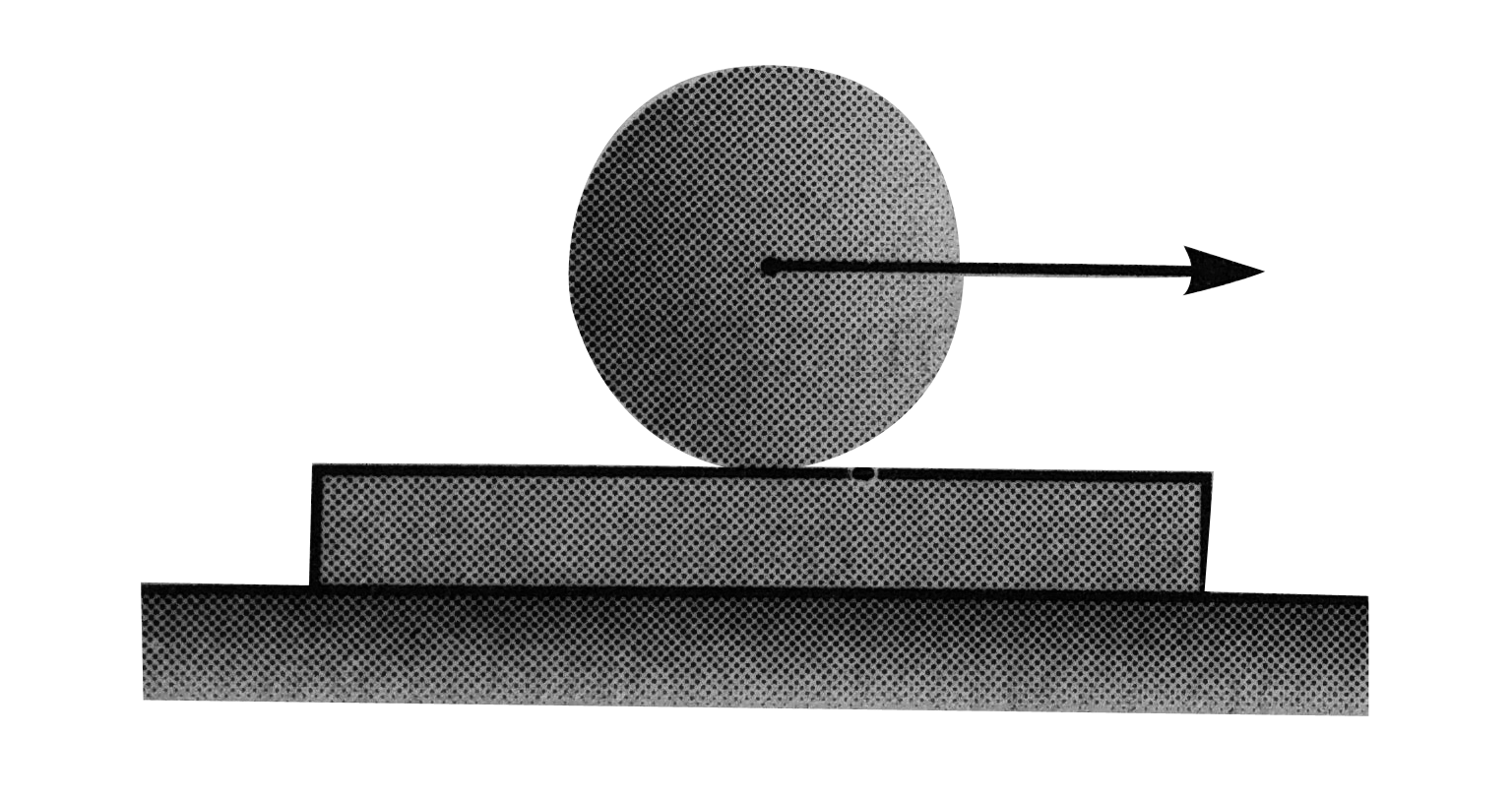
A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
ROTATIONAL MECHANICS
DC PANDEY|Exercise Level 1 Objective|30 VideosROTATIONAL MECHANICS
DC PANDEY|Exercise Level 1 Subjective|32 VideosROTATIONAL MECHANICS
DC PANDEY|Exercise Exercise 12.11|2 VideosROTATION
DC PANDEY|Exercise (C) Chapter Exercises|39 VideosROTATIONAL MOTION
DC PANDEY|Exercise Integer Type Questions|17 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY-ROTATIONAL MECHANICS-Assertion And Reason
- Assertion: Moment of inertia of a rigid body about any axis passing th...
Text Solution
|
- Assertion: A ball is released on a rough ground in the condition shown...
Text Solution
|
- Assertion: A solid sphere and a hollow sphere are rolling on ground wi...
Text Solution
|
- A small ball is released from rest from point A as shown. if bowl is s...
Text Solution
|
- Assertion: A cubical block is moving on a rough ground with velocity v...
Text Solution
|
- Assertion: A ring is rolling without slipping on a rough ground. It st...
Text Solution
|
- Assertion: There is a thin rod AB and a dotted line CD. All the axes w...
Text Solution
|
- Assertion: If linear momentum of a particle is constant, then its angu...
Text Solution
|
- In the figure shown A, B and C are three points on the circumference o...
Text Solution
|
- There is a triangular plate as shown. A dotted axis is lying in the pl...
Text Solution
|
- A horizontal force F is applied at the centre of solid sphere placed o...
Text Solution
|