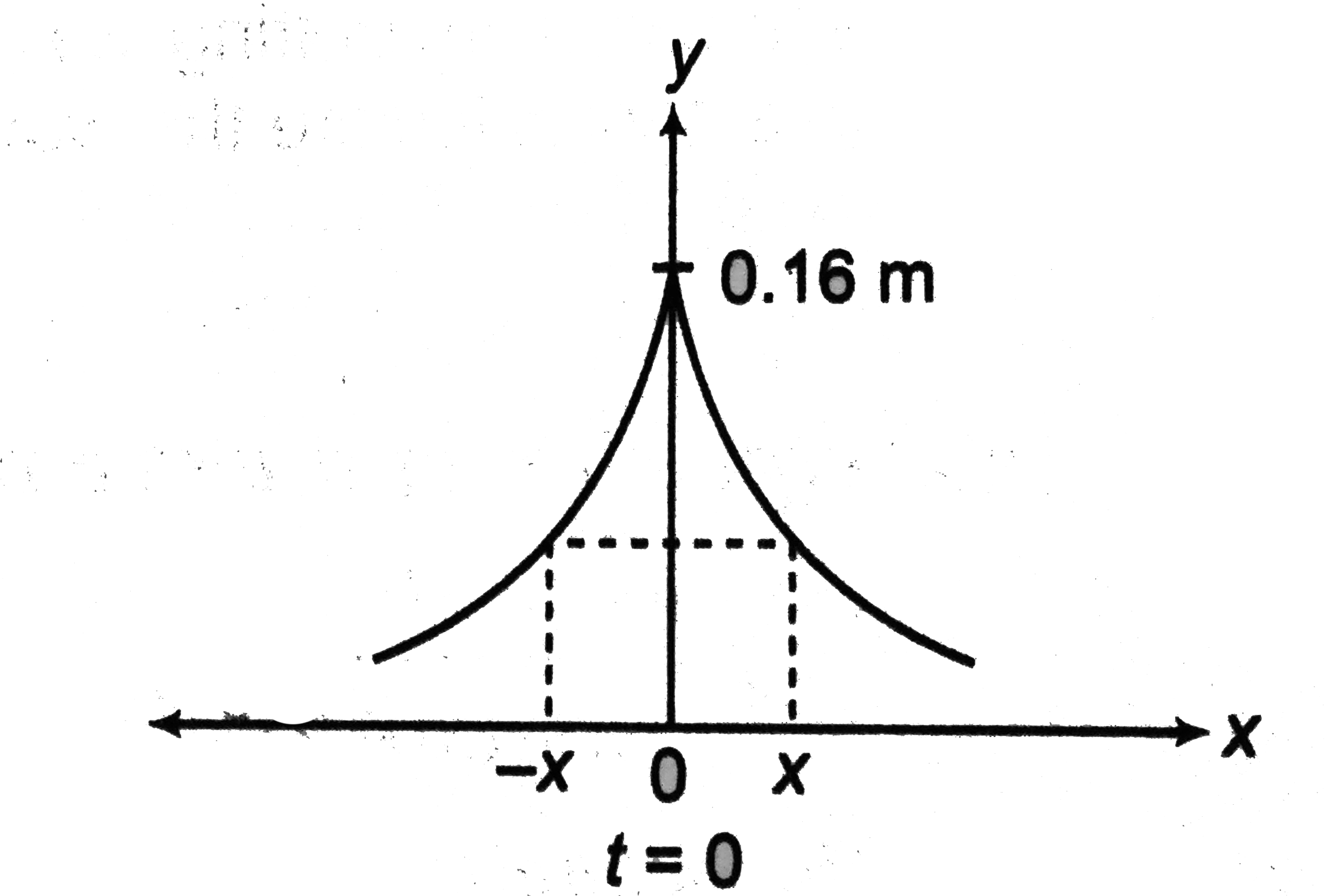
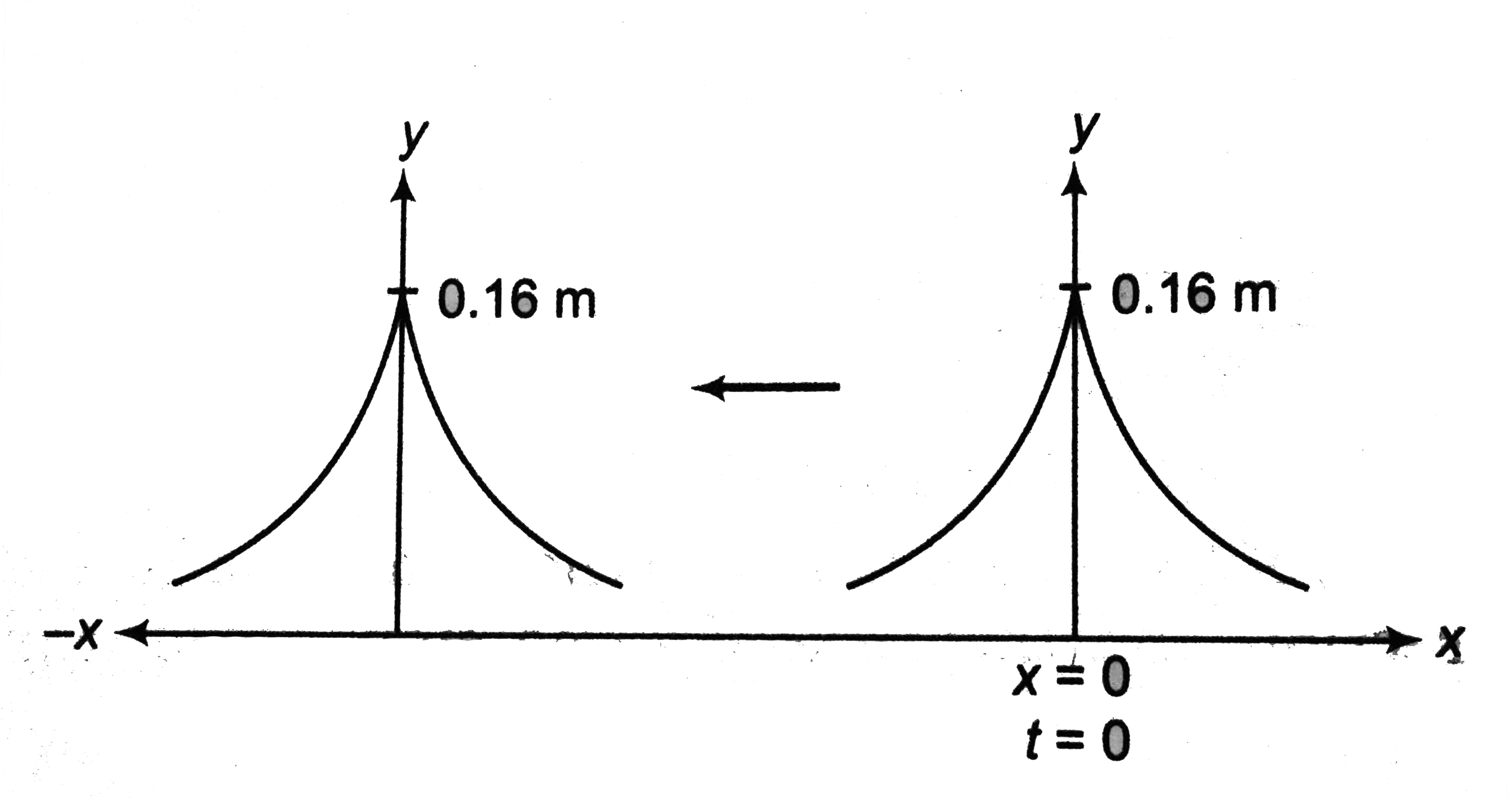
Text Solution
Verified by Experts
Topper's Solved these Questions
WAVE MOTION
DC PANDEY|Exercise Example Type 2|1 VideosWAVE MOTION
DC PANDEY|Exercise Example Type 3|1 VideosWAVE MOTION
DC PANDEY|Exercise Integer Type Question|11 VideosVECTORS
DC PANDEY|Exercise Medical enrances gallery|9 VideosWORK, ENERGY & POWER
DC PANDEY|Exercise Level 2 Comprehension Based|2 Videos
Similar Questions
Explore conceptually related problems