Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SOUND WAVES
DC PANDEY|Exercise Level 1 Assertion And Reason|10 VideosSOUND WAVES
DC PANDEY|Exercise Level 1 Objective|34 VideosSOUND WAVES
DC PANDEY|Exercise TYPE 5.|2 VideosSOLVD PAPERS 2017 NEET, AIIMS & JIPMER
DC PANDEY|Exercise Solved paper 2018(JIPMER)|38 VideosSUPERPOSITION OF WAVES
DC PANDEY|Exercise Level 2 Subjective|8 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY-SOUND WAVES-Miscellaneous Examples
- The water level in a vertical glass tube 1.0 m long can be adjusted to...
Text Solution
|
- A tube 1.0 m long is closed at one end. A stretched wire is placed nea...
Text Solution
|
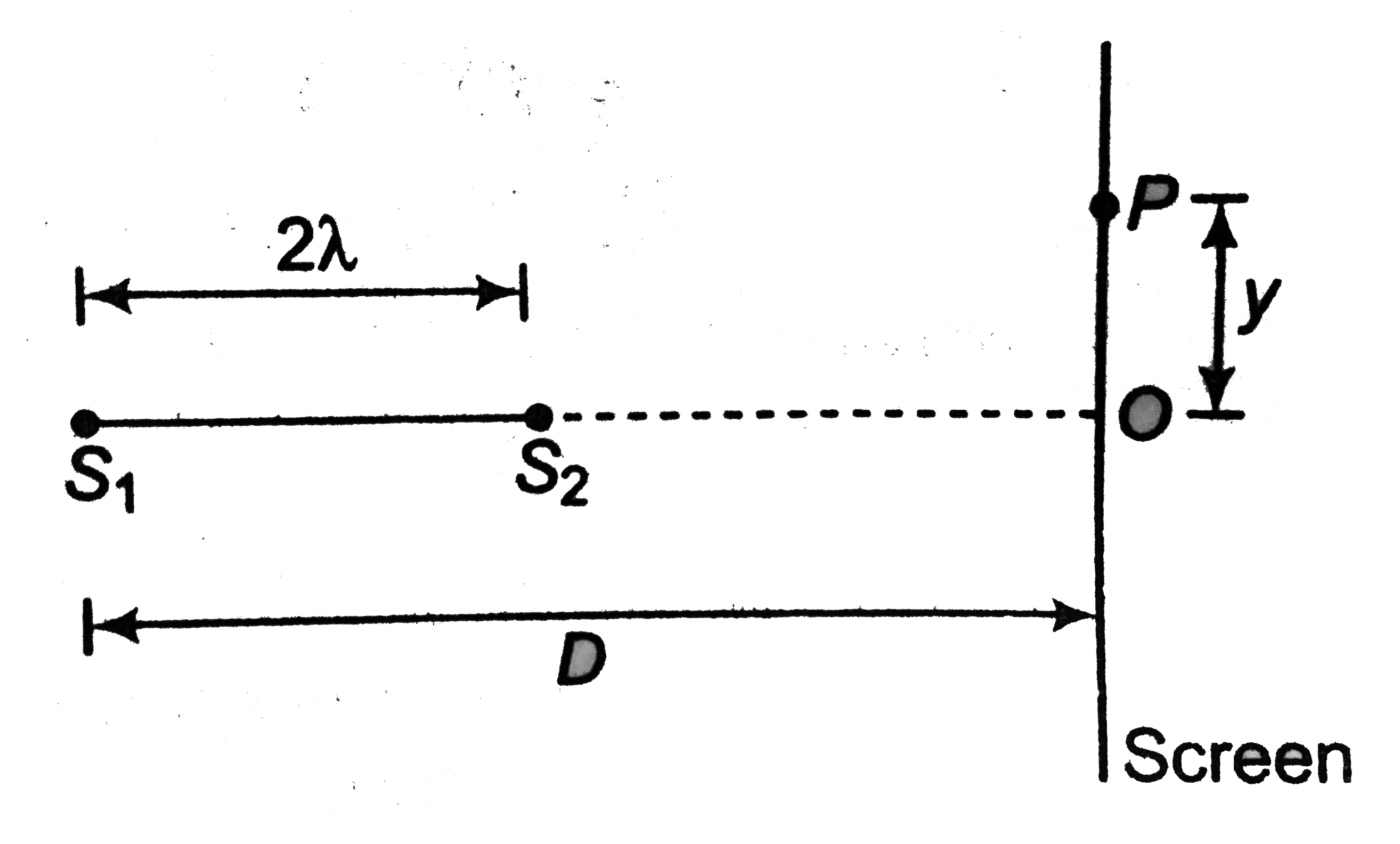
- Two coherent narrow slits emitting sound of wavelength lambda in the s...
Text Solution
|
- A fighter plane moving in a vertical loop with constant speed of radiu...
Text Solution
|
- A source of sound of frequency 1000 H(Z) moves unifornly along a stra...
Text Solution
|
- The air column in a pipe closed at one end is made to vibrate in its s...
Text Solution
|
- At a distance 20 m from a point source of sound the loudness level is ...
Text Solution
|
- A boat is travelling in a river with a speed 10 m//s along the stream ...
Text Solution
|