a. The equivalent capacitance
`C=(C_1C_2)/(C_1+C_2)`
or `C=((2)(3))/(2+3)=1.2muF`
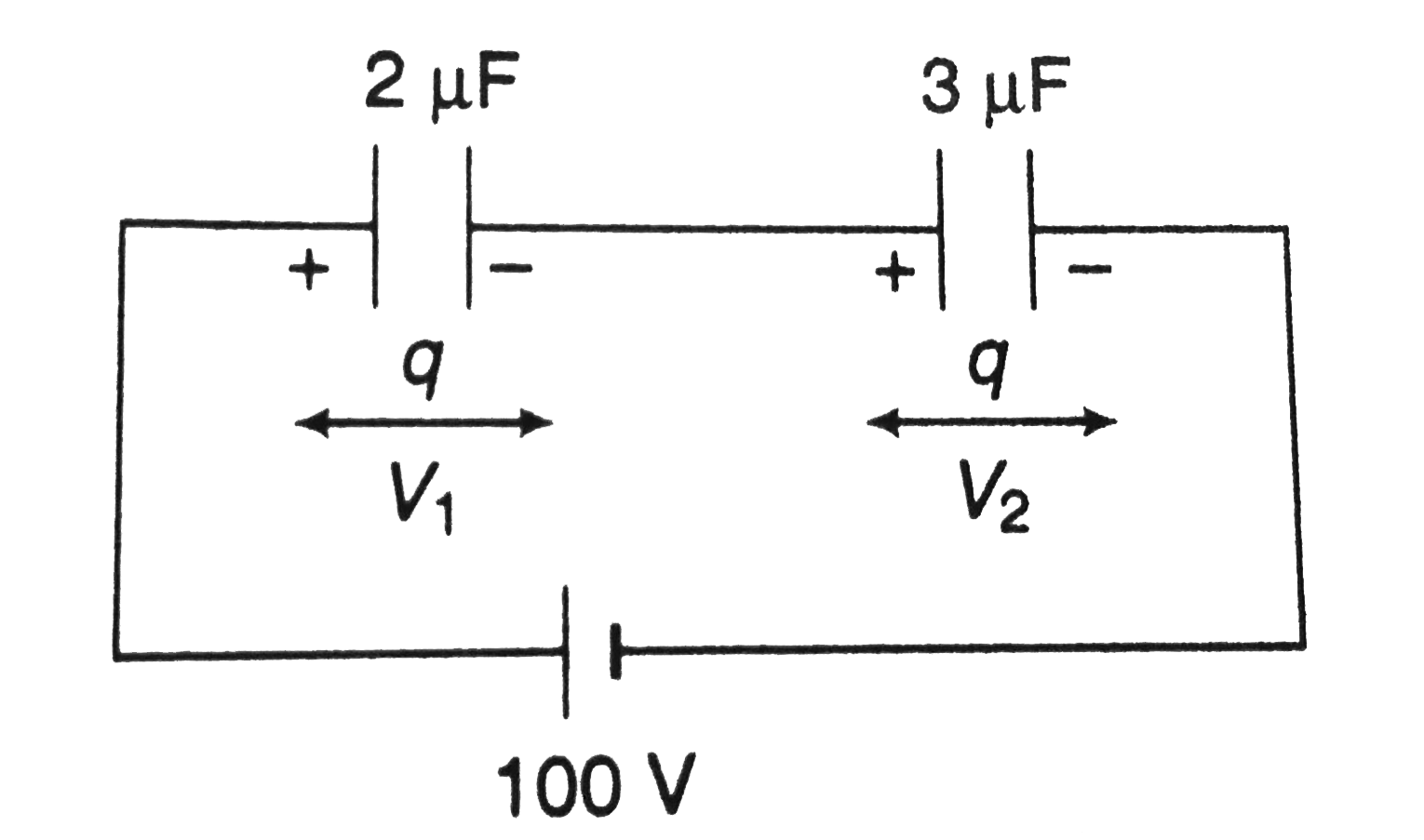
b. The charge `q` stored in each capacitor is
`q=CV=(1.2xx10^-6)(100)C`
`=120muC`
c. In series combination `Vprop1/C or V_1/V_2=C_2/C_1`
`:. V_1=(C_2/(C_1+C_2))V+((3)/(2+3))(100)=60V`
`and V_2=V-V_1 =100-60=40V` ltbr In parallel
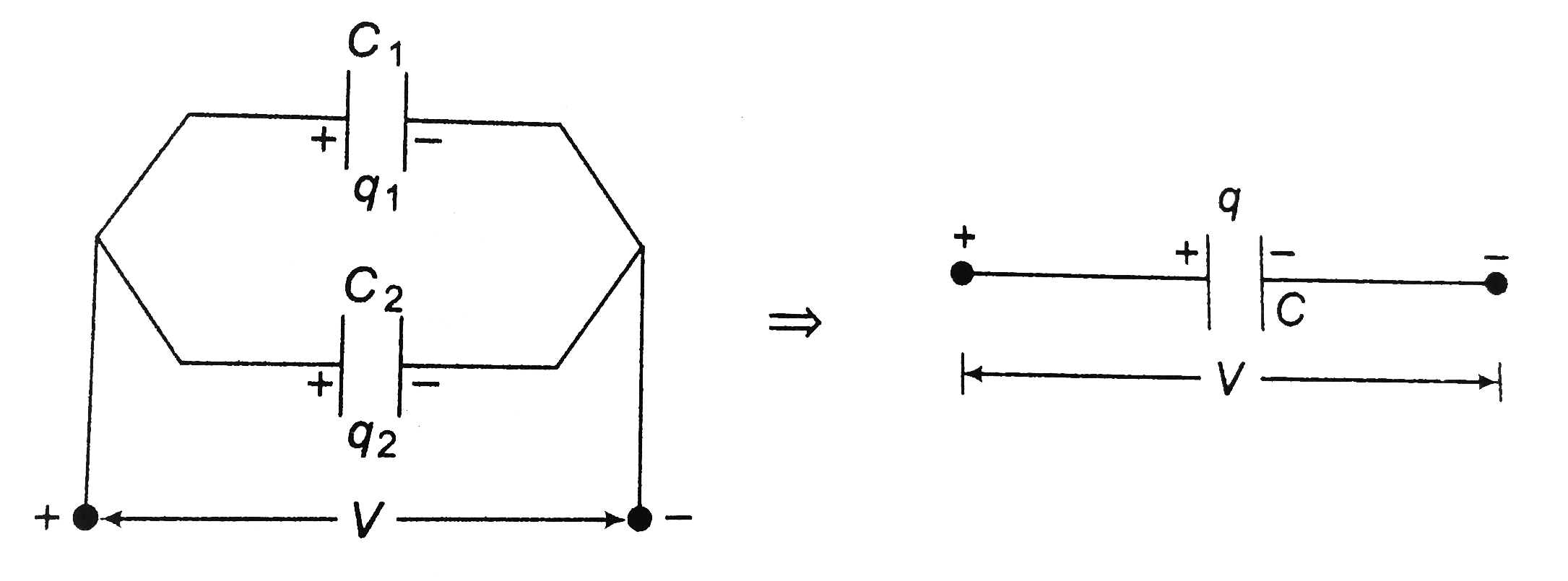
the arrangement shown in figure is called a paralel connection. In a parallel combination the potential difference for all individual capacitors is the same and the total charge `q` is distributed in the ratio of the capacities. (as`q=CV` or `qpropC` for same potential difference). Thus,
`q_1/q_2=C_1/C_2`
or `q_1=((C_1)/(C_1+C_2))q and q_2=((C_2)/(C_1+C_2))q`
The parallel combination is equivalent to a single capacitor with the same total charge `q=q_1+q_2` and potential difference V.
Thus,
`q=q_1+q_2`
or `CV=C_1+C_2V`
or `C=C_1+C_2`
In the same way, we can show that for any number of capacitors in parallel
`C=C-1+C_2+C_3+..........`
In a parallel combination the equilavent capacitance is always greater than any individual capacitance.