Let the charges in three capacitors be as shown in figure.
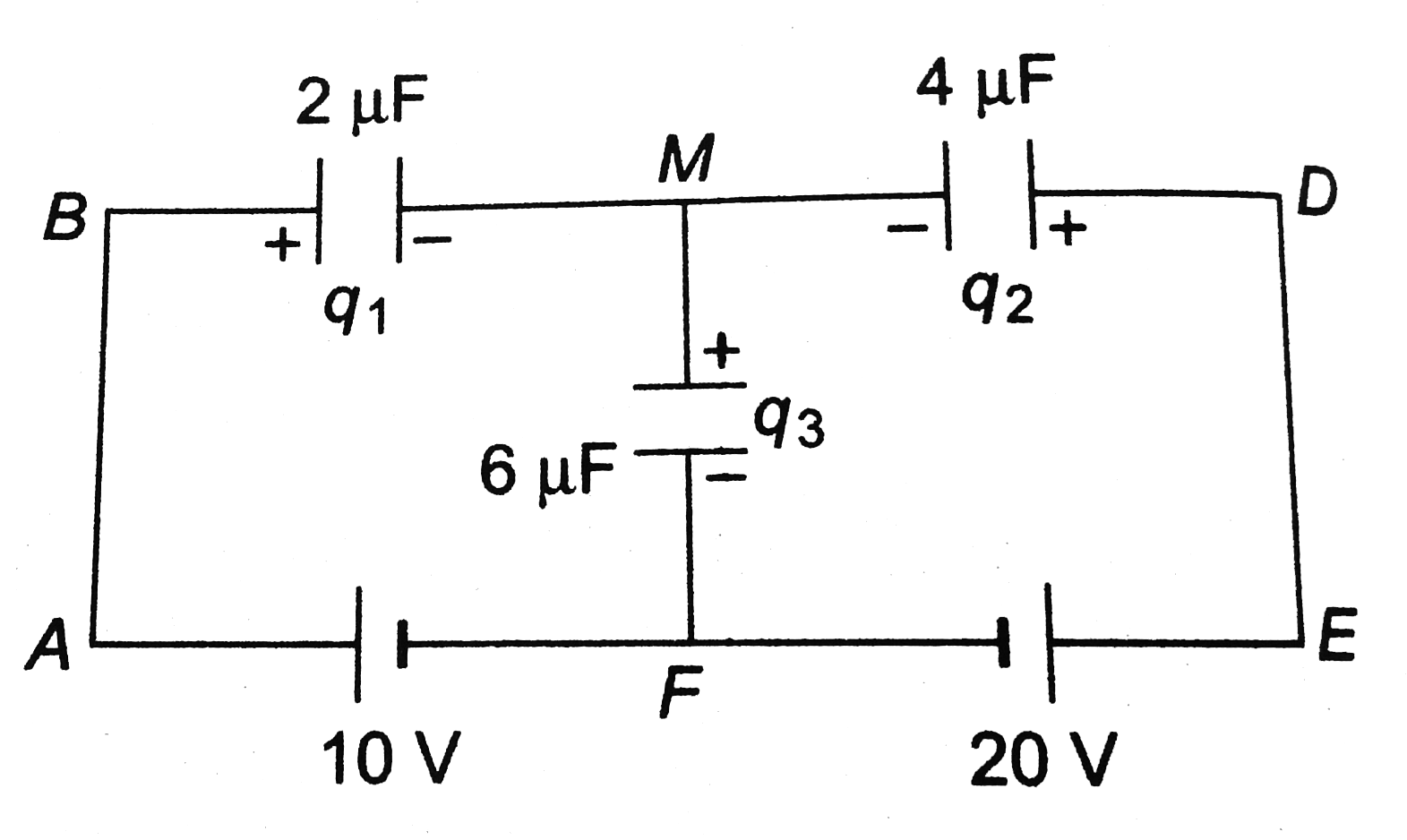
Charge supplied by `10 V` battery is `q_1` and that from `20 V` battery is `q_2`. Thus,
`q_1+q_2=q_3`…….i
This relation can also be obtained by a different method. The charge on the three plates which are in contact add to zero. Because these plates take together form an isolated system which can't receive charges from the batteries. Thus,
`q_3-q_1-q_2=0`
or `q_3=q_1+q_2`
Applying second law in loops `BMFAB` and `MDEFM`, we have
`-q_1/2-q_3/6+1=0`
or ` q_3+3q_1=60`........ii
and `q_2/4-20+q_3/6=0`
or `3q_2-20+q_3/6=0`............iii
Solving the above three equations we have
`q_1=10/3muC`
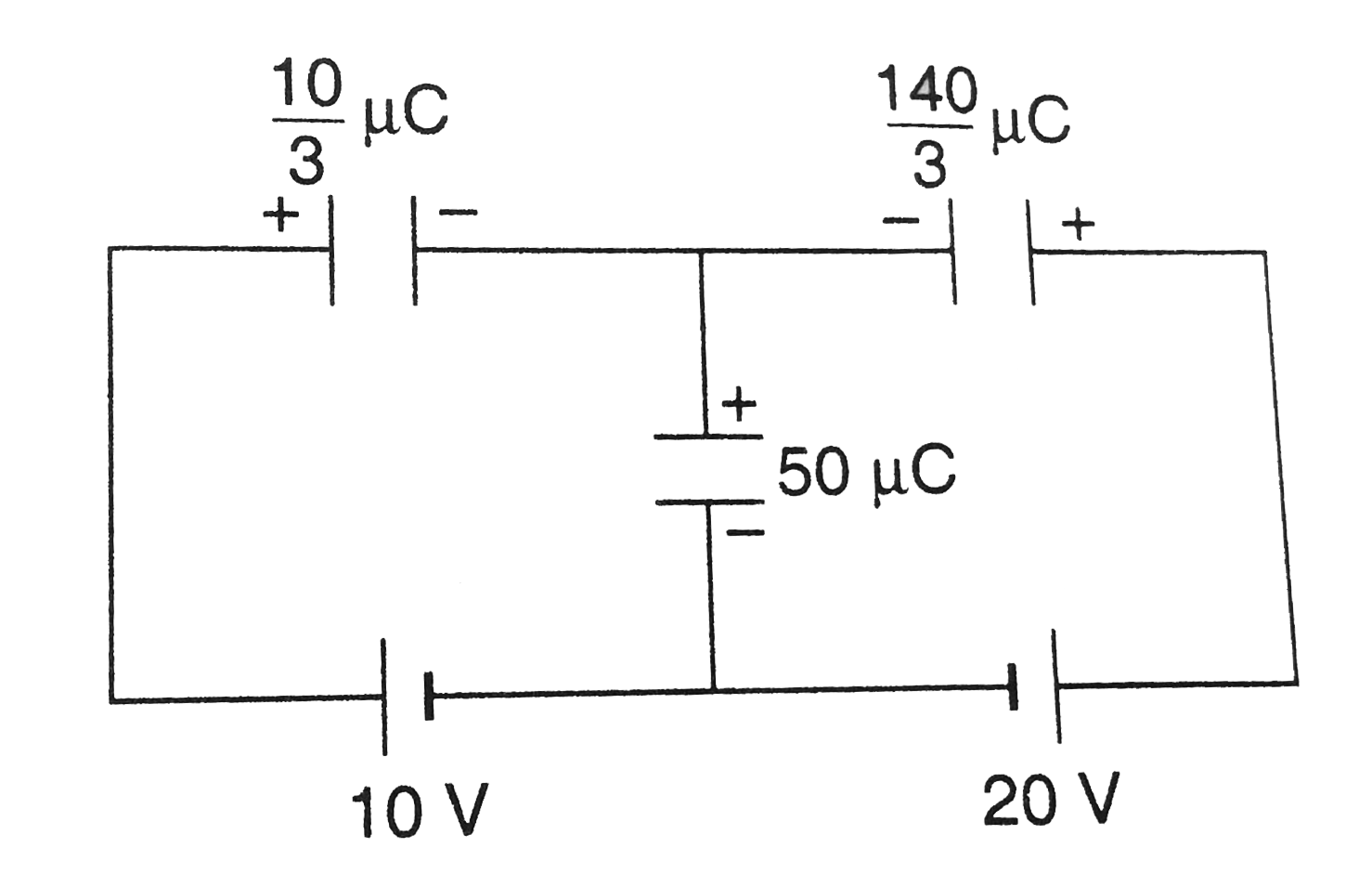
`q_2=140/3muC`
and `q_3=50muC`
Thus, charges on different capacitors are as show in figure.