a. Electri field is uniform between the plates of the capacitor. The magnitude of this field is
`E=sigma/epsilon_0-q/(Aepsilon_0)`
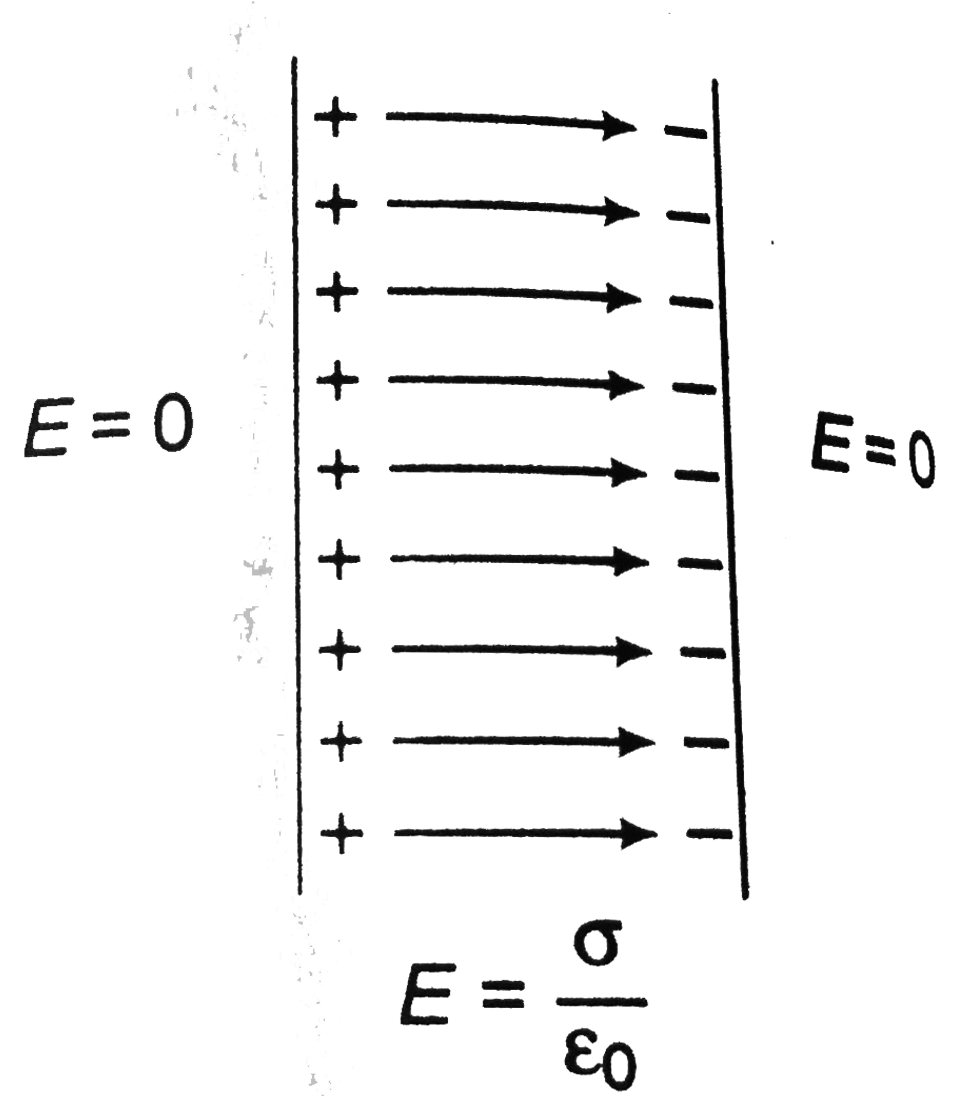
Therefore, the energy density `u` should also be constant.
`u=1/2epsilon_0E^2=q^2/(2A^2epsilon_0)`
`:.` Total stored energy,
`U=(u)(t o tal volume)`
`=(q^2)/((2A^2epsilon_0))(A.d)=q^2/(2((Aepsilon_0)/d))`
`=q^2/(2C)`
`:. U=q^2/(2C)`
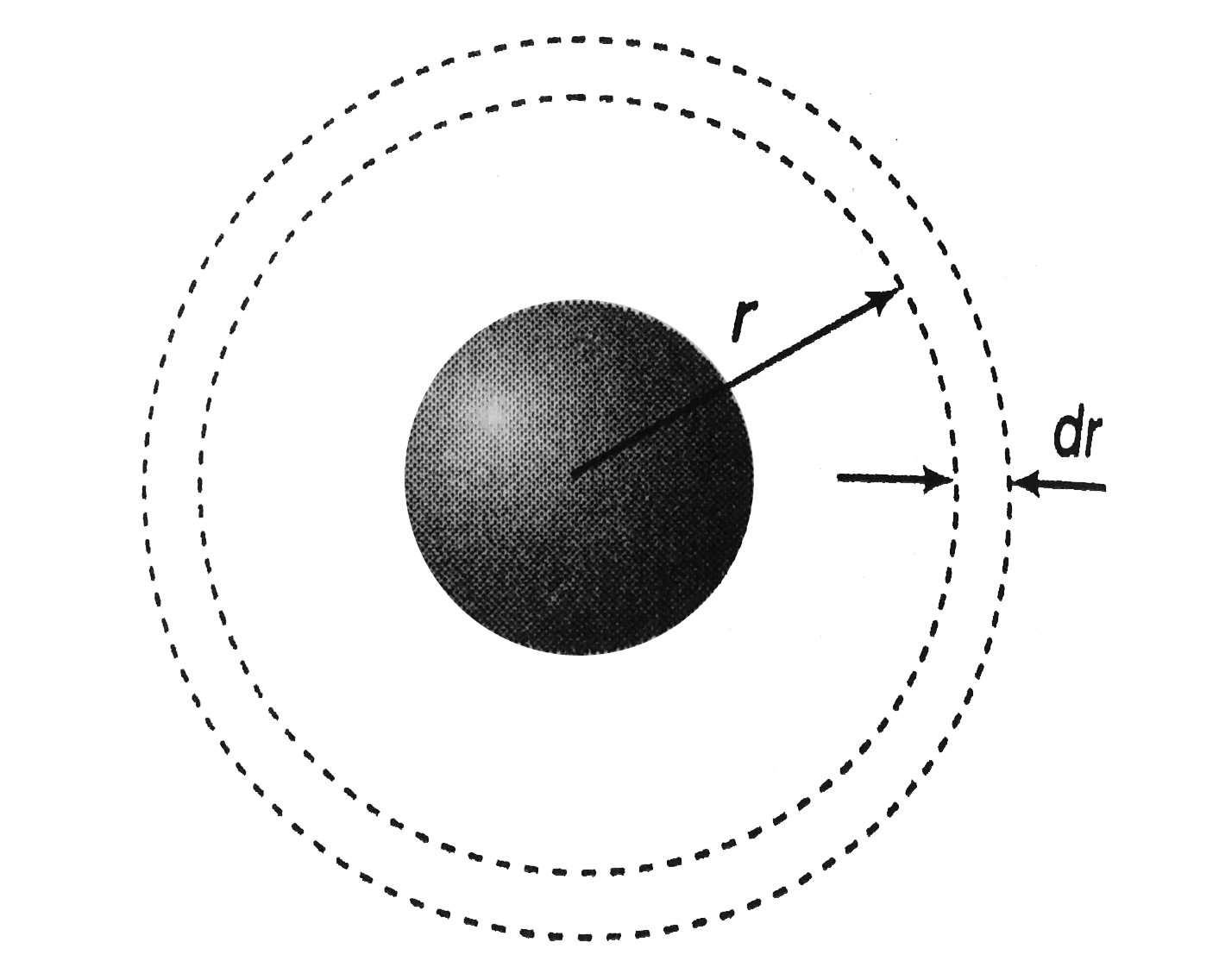
b. In case of a sphereical conductor (of radius `r`) the excess charge resides on the surface of the conductor. The field inside conductor is zero if extends from surface to infinity. And since the potential energy is stored in the field only, it will be stored in the region extgending from surface to infinity. But as the field is non uniform the energy density `u` is also no uniform. so, the total energy will be calculated by integration. Electric field at a distance r from the centre is
`E=1/(4piepsilon_0).q/r^2`

`:. u(r)=1/2epsilon_0E^2`
`=1/2epsilon_0{1/(4piepsilon_0).q/r^2}^2`
energy stored i a volumn `dV=(4pir^2)dr` is
`dU=udV`
`:.` total energy strored, `U=int_(r=R)^(r=oo)dU`
Substituting the values, we get
`U=q^2/(2(4piepsilon_0R))`
or `U=q^2/(2C)`
(as `C=4piepsilon_0R`)