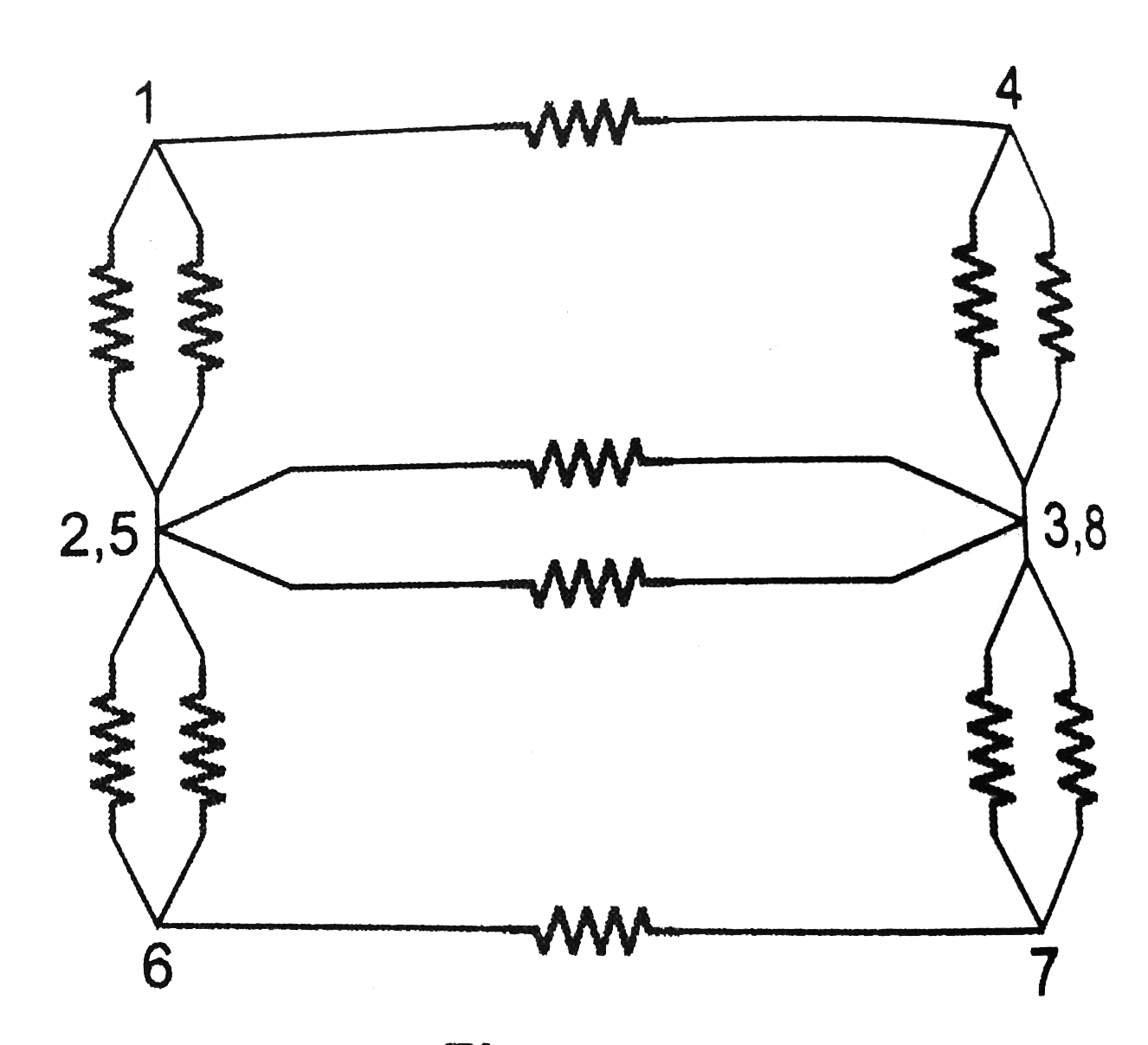
a. Between 1 and 4: Points 2 and 5 are symmetrically located w.r.t points 1 and 4. so, they are at same potentials
similarly points 3 and 8 also symmetircally located w.r.t point 1 and 4. So they are again at same potential. Now, we have 12 resistors each of resistance r connected across 1 and 2, 2 and 3,...., etc. So redrawing them wiht the assumption that 2 and 5 are at same ptential and 3 and 8 are at same potential. The new figure is a shown in figure.
Now we had to find the equivalent resistance between ltbr. 1 and 4. We can now simplify the circuit as
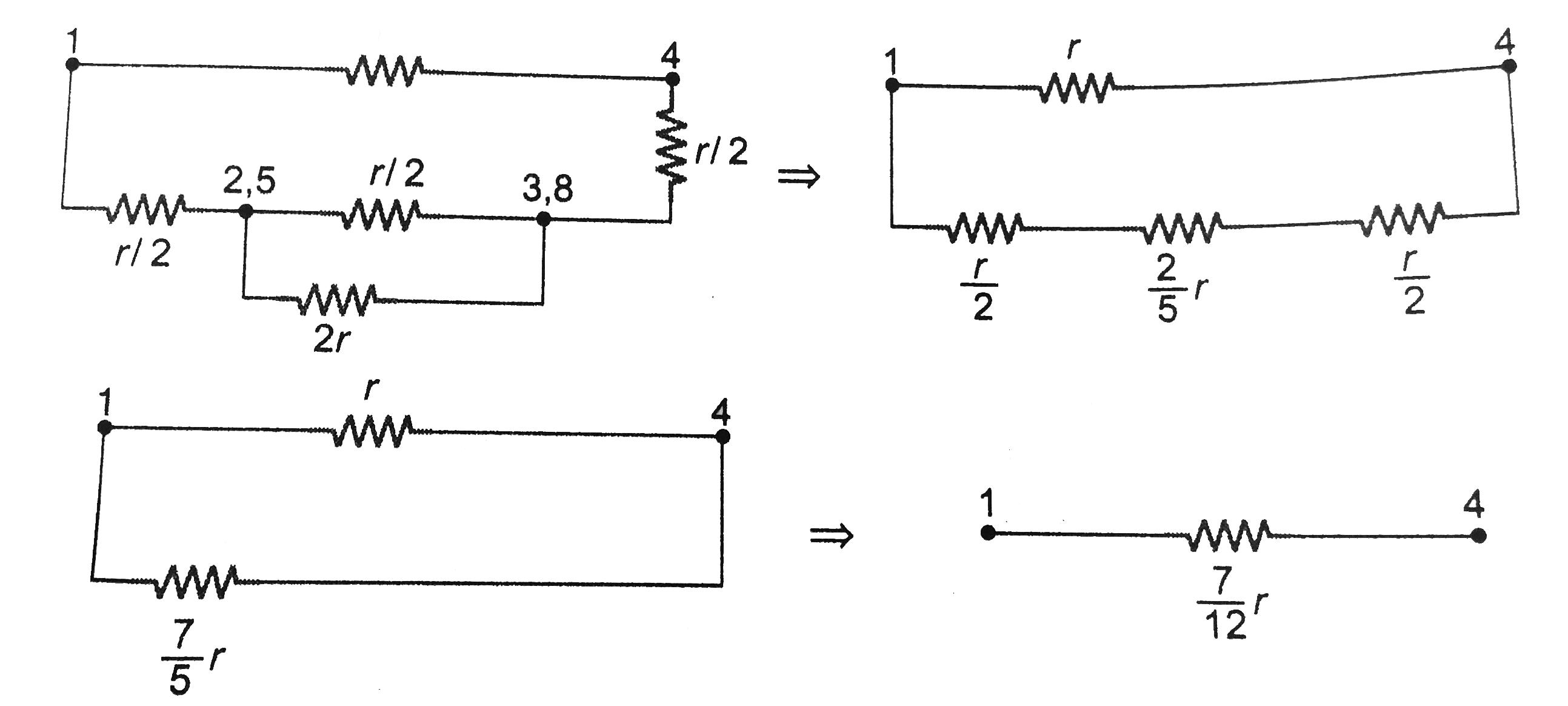
Thus, the equivalent resistance between points 1 and 4 is `7/12 r`.
b. Between 1 and 3: Points 6 and 8 are symmetrically located w.r.t points 1 and 3. Similarly points 2 and 4 are located symmetrically w.r.t points 1 and 3. So, points 6 and 8 are at the same potential. similarly 2 and 4 are at same potentials. Redrawing the simple circuit we have figure.
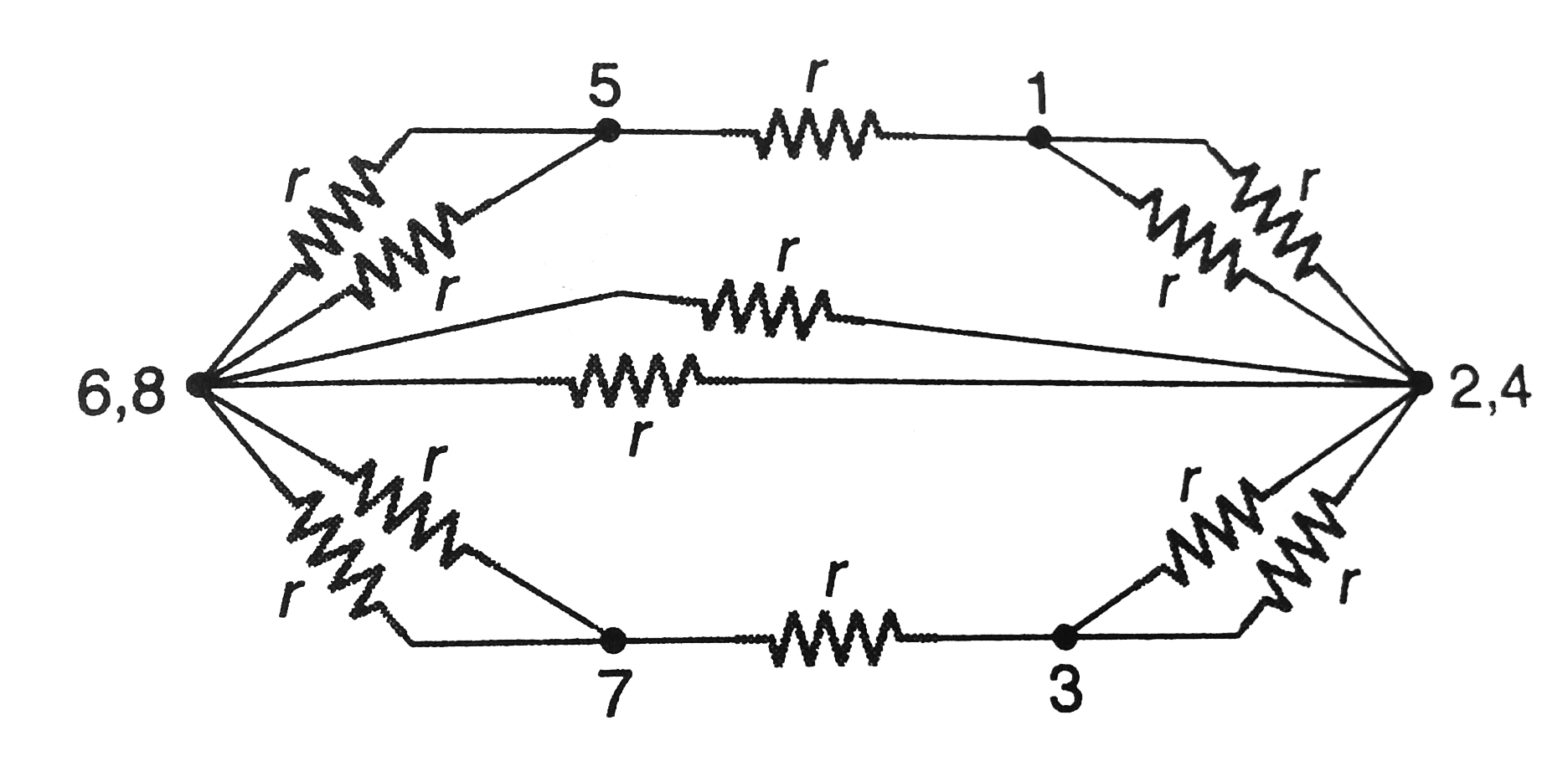
Between 1 and 3, a balanced Wheatstone bridge is formed as shown in figure. So, the resistance betwen 2 and 6 and between 4 and 8 can be removed.
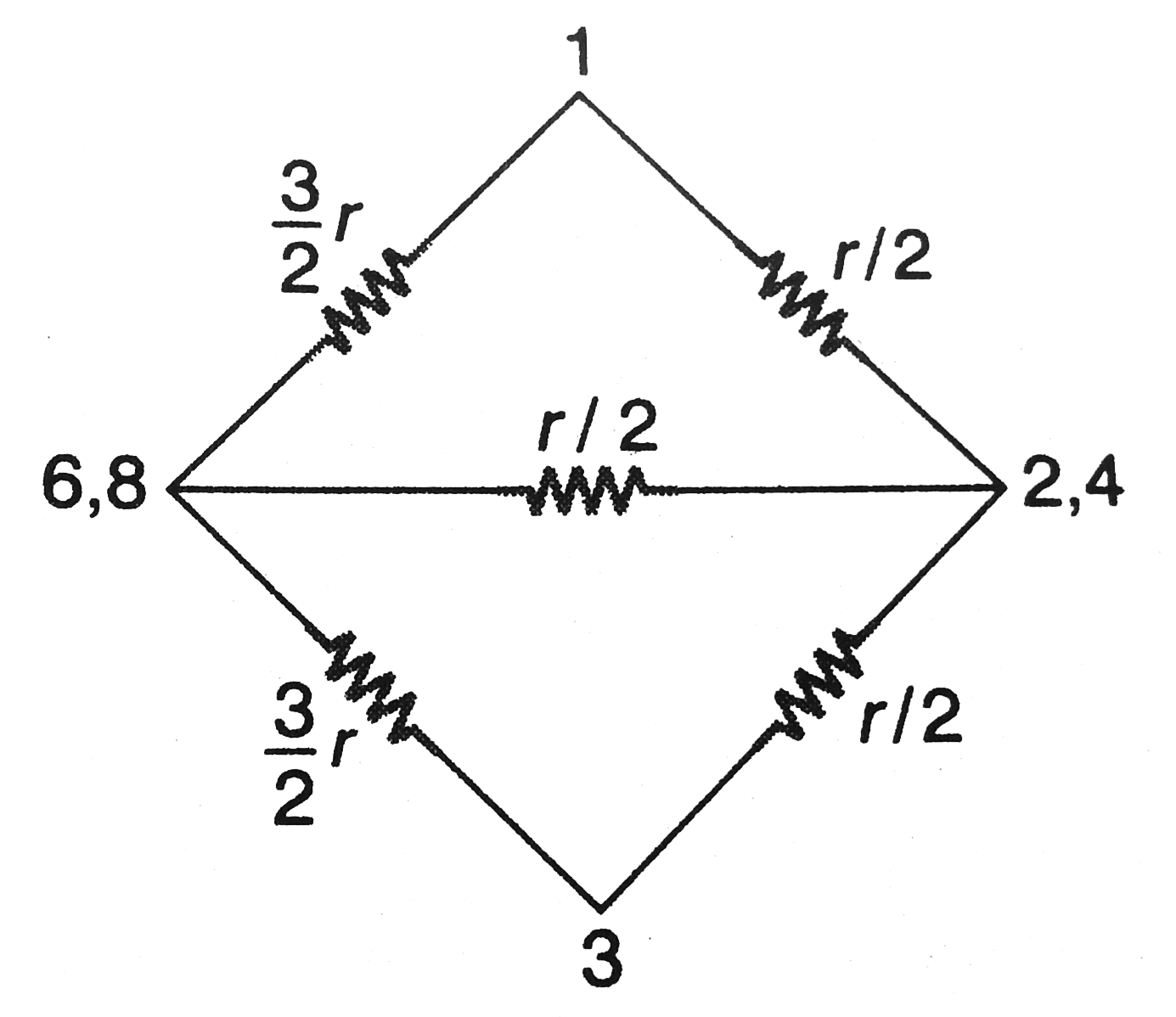
Thus, the equivalent resistance between 1 and 3 is `3/4r`