Home
Class 12
PHYSICS
In the circuit shown in figure-3.240 swi...

In the circuit shown in figure-3.240 switch S is closed at time t=0. find the current through different wires and charge stored on the capacitor at any time t.

Text Solution

Verified by Experts

Calculation of `tau_C` Equivalent resistance across capacitor after short circuiting the battery is

`R_(n et)=(R+(6R)(3R))/(6R+3R)=3R`
`tauC=(C)R_(net)=3RC`
Calculation of steady state charge `q_0` at `t=oo` capacitor is fully charged and no current flows through it.

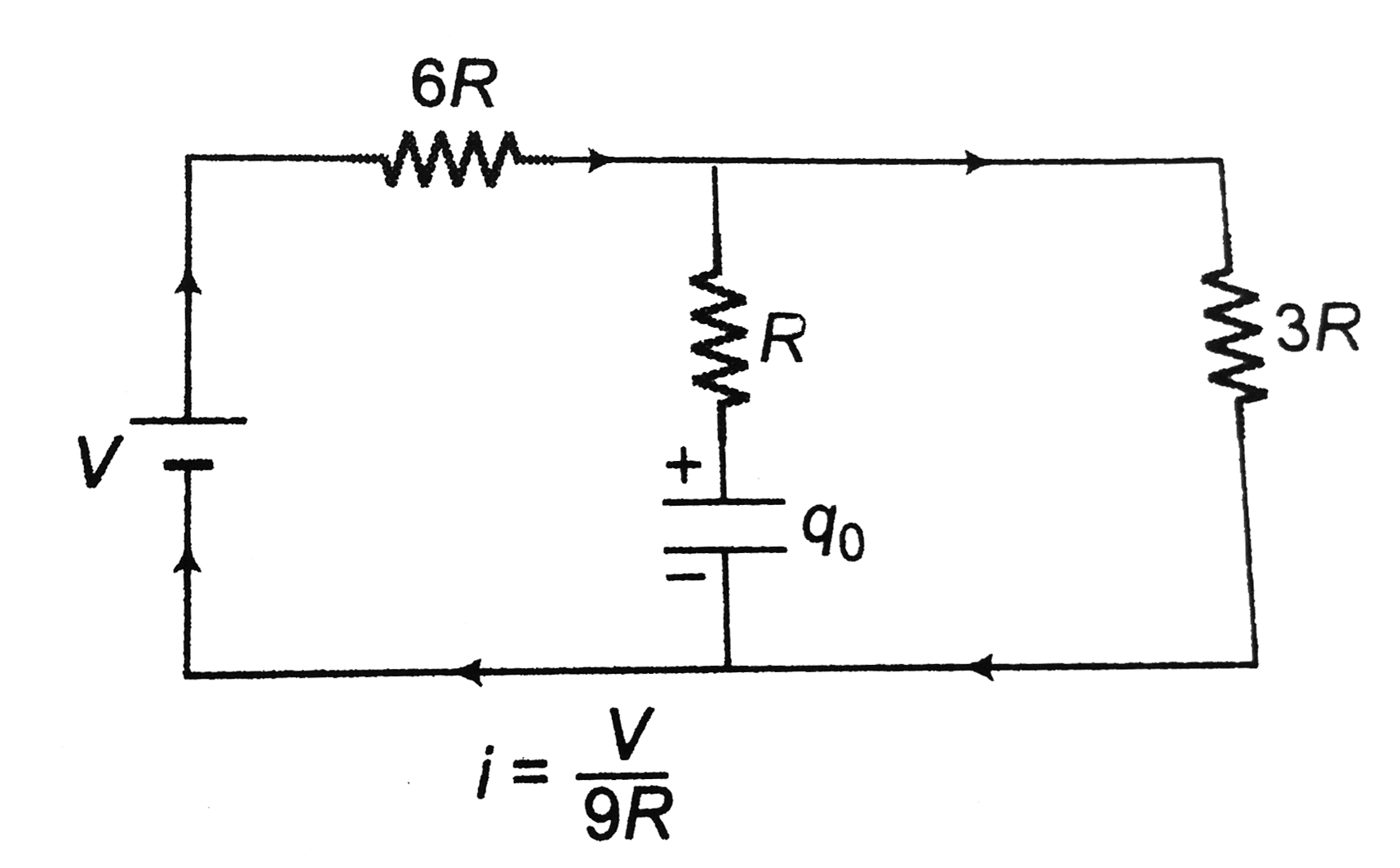
`=(V/(9R))(3R)`
`=V/3`
`q_0=(CV)/3`
Now, let charge on the capacitor at any time `t` be `q` and current through it is `i_1`. Then, `q=q_0(1-e^(-t/(tauC)))`...........i
Applying Kirchoff's second law in loop ACDFA,we have

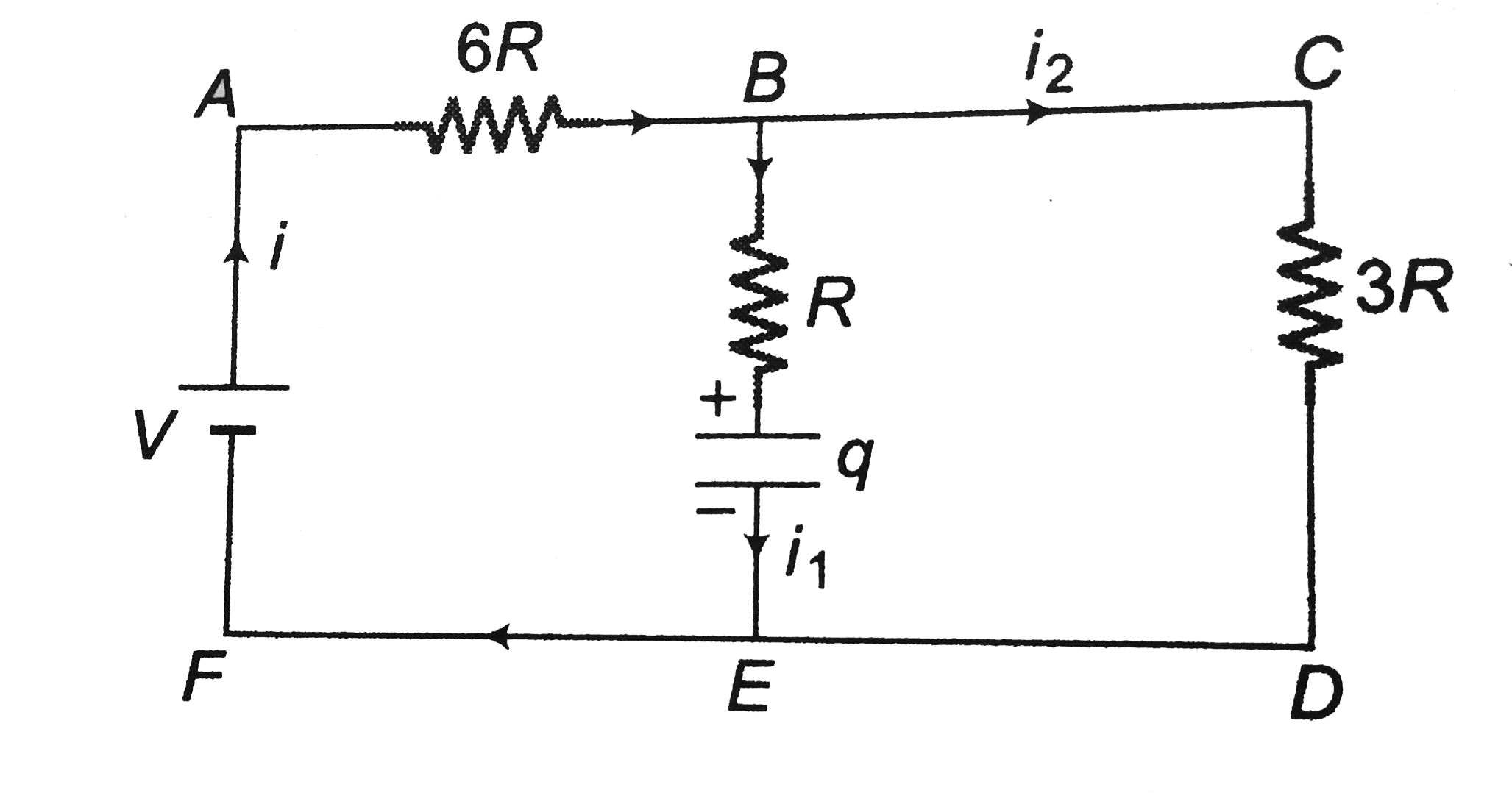
`-6ir-3i_2R+V=0`
or `2i+i_2=V/(3R)` ............ii
Apply Kirchoff's junction law at B,we have
`i=i_1+i_2` ..............iii
Solving eqn i , ii and iii we have
`i_2=V/(9R)-2/3i_1=V/(9R)-(2q_0)/(3tau_C)e^(-t/(tauC))` and `i=V/(9R)+q_0/(3tau_C)e^(-t/(tau_C))`
Promotional Banner

Topper's Solved these Questions

  • CAPACITORS

    DC PANDEY|Exercise Exercise|155 Videos

  • CAPACITORS

    DC PANDEY|Exercise OBJECTIVE_TYPE|1 Videos

  • ATOMS

    DC PANDEY|Exercise MEDICAL ENTRANCES GALLERY|42 Videos

  • COMMUNICATION SYSTEM

    DC PANDEY|Exercise Subjective|11 Videos

Similar Questions

Explore conceptually related problems

In the circuit shown in the figure, switch S is closed at time t=0 . Select the correct statements.

In the circuit shown in figure switch S is closed at time t=0 Current I from the battery at time t is given by

In the circuit shown in figure switch S is closed at time t=0 At what time current through 3Omega resistance and 1H inductor are equal?

In the circuit shown in the figure, switch S is closed at time t = 0 . (a) Write current in the circuit and charge on capacitor as a function of time. Draw the graphical plot for the same. (b) Find maximum charge on the capacitor. What is potential difference across the inductor when charge on the capacitor is maximum?

In given LR circuit the switch S is closed at time t=0 then

In the circuit shown in figure, circuit is closed at time t=0 . At time t=ln(2) second

Switch S is cloesd in the circuit at time t = 0 . Find the current through the capacitor and the inductor at any time t

In the circuit shown, switch S is closed at time t = 0 . Find the current through the inductor as a function of time t .

In the circuit shown in figure switch S is closed at time t=0 . The charge which passes through the battery in one time constant is

In the circuit shown in figure switch S is closed at time t=0, which statement is true after one time constant of L-R circuit?