A loop is formed by two parallel conductors connected by a selenoid with inductance `L` and a condutcing rod of mass which can freely (without friction) slide over the conductors. The conductors are located `i` a horizontal plane in as uniform vertical magnetic field `B`.The distance between the conductors is `l`.

At the moment `t=0` the rod is impaert dan initial velocity `v_0` directed to the right. find the law of its motion `d(t)` if the electric resistance of the loop is negligible

Explanation

Let at any instant of time velocity of the rod is `v` towards right. The current in the circuit is `i`. In the figure.

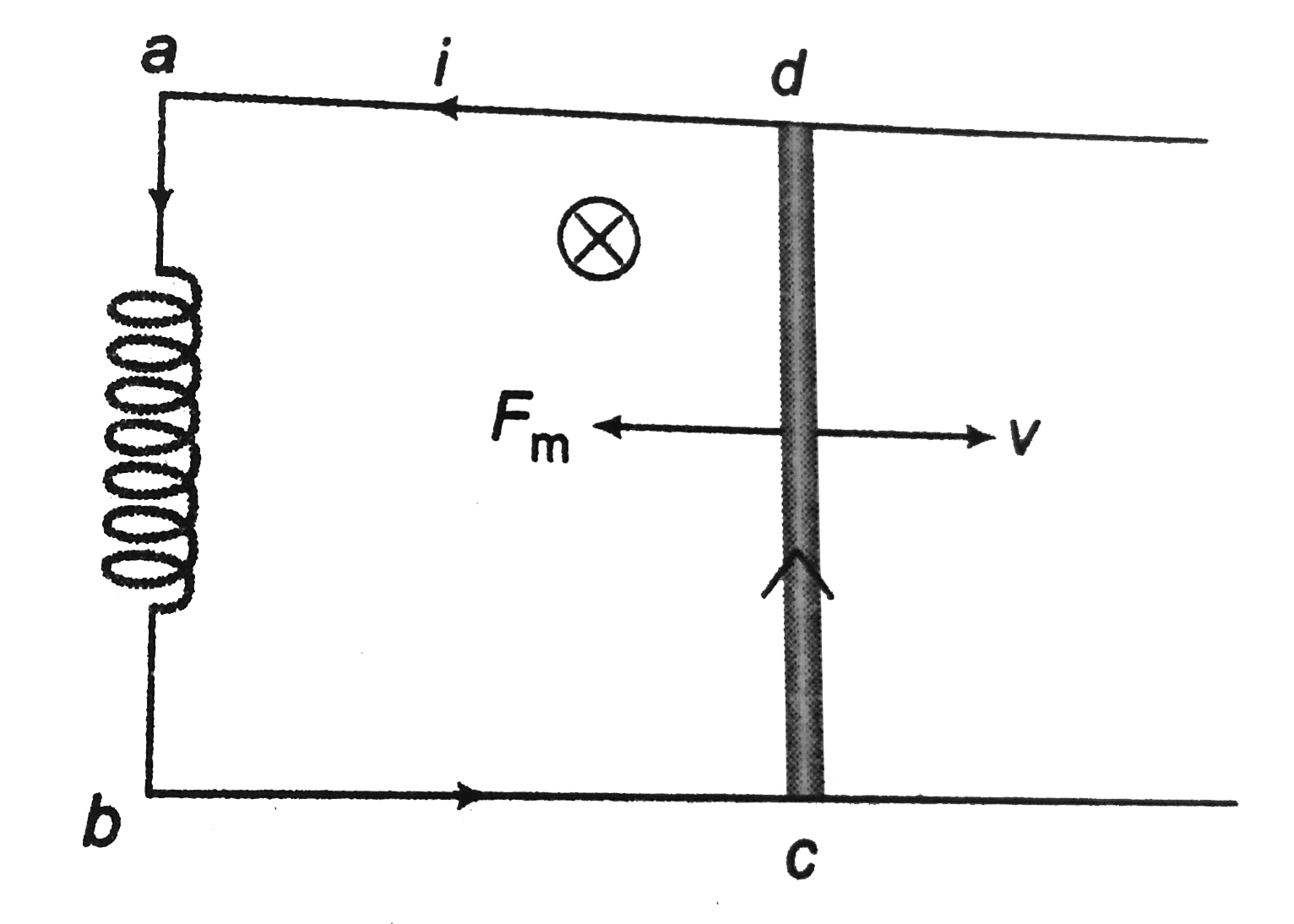
`V_a-V_b=V_d-V_c`
or `L=(di)/(dt)=Bvl=Bl(dx)/(dt)` ( as `v=(dx)/(dt))`
i.e., `Ldi=Bldx`
Integrating on both side we get
`Li=Blx`
or `i=(Bl)/Lx`..........i
Magnetic fore on the rod at this instant is
`F_m=ilB=(B^2l^2)/Lx`............ii
Since, this force is in opposite direction of `v`, so from newton's second law we can write
`m((d^2x)/(dt^2))=-(B^2l^2)/Lx`
or `((d^2x)/(dt^2))=-(B^2l^2)/(mL)x`
comparing this with equation of `SHM`,
`(d^x)/(dt^2)=-omega^2x`
We have `omega=(Bl)/sqrt(mL)`
Therefore, the rod will oscillate simple harmonically with angular frequency `omega=(Bl)/sqrt(mL)`. At time `t=0`, rod was at `x=0` and it was moving towards positive x-axis.Hence `x-t` equation of the rod is
`x=Asinomegat`.........iii
To find `A` , we use the fact that at `t=0, v` or `(dx)/(dt)` has a value `v_0`. Hence,
`(dx)/(dt)=v=Aomegacosomegat`
or `Aomega=v_0`(at `t=0)`
or `A=v_0/omega`
substitutng in Eqn iii we have
`x=v_0/omegasinomegat`, where `omega=(Bl)/sqrt(mL)`
At `x = A,v = 0` i.e. whole of its kinetic energy is converted into magnetic energy. Thus,
`(1)/(2)Li^(2) = (1)/(2) mv_(0)^(2)`
Substituting value of i from Eq. (i), with `x = A`, we have
`L((Bl)/(L)A)^(2) = mv_(0)^(2)`
or `A = (sqrt(mL))/(Bl) v_(0) = (v_(0))/(omega)`
as `omega =(Bl)/(sqrt(mL))`