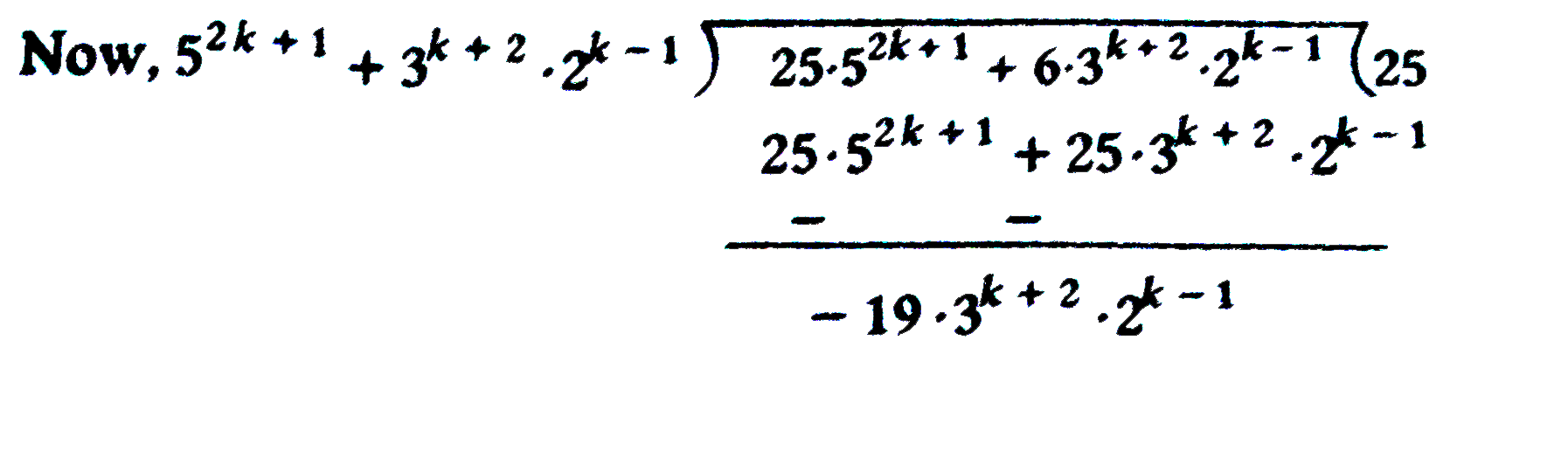Home
Class 12
MATHS
Use the principle of mathematical induct...

Use the principle of mathematical induction to show that `5^(2n+1)+3^(n+2).2^(n-1)` divisible by 19 for all natural numbers n.

Text Solution

Verified by Experts

Let `P(n)=5^(2n+1)+3^(n+2).2^(n-1)`
Step I For `n=1,P(1)=5^(2+1)+3^(1+2).2^(1-1)=125+27=152`, which is divisible by 19.
Step II Assume that the result is true for `n=k`, i.e.,
`P(k)=5^(2k+1)+3^(k+2).2^(k-1)` is divisible by 19.
`rArr P(k)=19r`, where r is an integer .
Step III for `n=k+1`.
`P(k+1)=5^(2(k+1)+1)+3^(k+1+2).2^(k+1-1)`
`5^(2k+3)+3^(k+3).2^(k)`
`=25.5^(2k+1)+3.3^(k+2).2.2^(k-1)`
`=25.5^(2k+1)+6.3^(k+2).2^(k-1)`

`therefore 25.56(2k+1)+6.3^(k+2).2^(k-1)=25.(5^(2k+1)+3^(k-2).2^(k-2))-19.3^(k+2).2^(k-1)`
i.e., `P(k+1)=25P(k)-19.3^(k+2).2^(k-1)`
But we know that P(k) is divisible by 19. Also , `19.3^(k+2).2^(k-1)` is clearly divisible by 19.
Therefore , `P(k+1)` is divisible by 19. This shows that the result is true for `n=k+1`.
Hence , by the principle of mathematical induction , the result is true for all `n in N`.
Promotional Banner

Topper's Solved these Questions

  • MATHEMATICAL INDUCTION

    ARIHANT MATHS|Exercise Mathematical Induction Exercise 1: (Single Option Correct Tpye Questions)|3 Videos

  • MATHEMATICAL INDUCTION

    ARIHANT MATHS|Exercise Exercise (Statement I And Ii Type Questions)|3 Videos

  • LOGARITHM AND THEIR PROPERTIES

    ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|4 Videos

  • MATRICES

    ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|49 Videos

Similar Questions

Explore conceptually related problems

Use the principle of mathematical induction to show that a^(n) - b^9n) is divisble by a-b for all natural numbers n.

Using principle of mathematical induction prove that x^(2n)-y^(2n) is divisible by x+y for all nN.

Using the principle of mathematical induction, prove that (7^(n)-3^(n)) is divisible by 4 for all n in N .

Using the principle of mathematical induction, prove that (2^(3n)-1) is divisible by 7 for all n in N

Using the principle of mathematical induction. Prove that (x^(n)-y^(n)) is divisible by (x-y) for all n in N .

Prove by Principle of Mathematical Induction that (10^(2n -1) + 1) is divisible by 11 for all n in N .

Prove by the principle of mathematical induction that n(n+1)(2n+1) is divisible by 6 for all n in N

Using mathematical induction, prove that for x^(2n-1)+y^(2n-1) is divisible by x+y for all n in N

Using the principle of mathematical induction, prove that n<2^(n) for all n in N