`aKIO_(3)+bKI+cH_(2)SO_(4)rarrdKI_(3)+eK_(2)SO_(4)+fH_(2)O`
`a+b=d+2e`(balancing the `K` atoms)…(i)
`a+b=3d`(balancing the `I` atoms)…..(ii)
`c=e=f`(balancing the `H` and the `S` atoms)……(iii)
`3a+4c=4e+f`(balancing the `O` atoms)….(iv)
Combining equations (iii) and (iv)
`3a=f`
Let `a=1`, then `c=e=f=3`
Substracting equation (i) from equation (ii)
`d=e=3`
Hence, `b=3(3)-1=8`
The combination equation is
`KIO_(3)+8KI+3H_(2)SO_(4)-3KI_(3)+3K_(2)SO_(4)+3H_(2)O`
b. `aPb(N_(3))_(2)+bCo(MnO_(4))_(3)rarrcCoO+dMnO_(2)+ePb_(3)O_(4)+fNO`
`:. a= 3e`(balancing `Pb` atoms)....(i)
`6a=f`(balancing `N` atoms).....(ii)
`b=c`(balancing `Co` atoms)....(iii)
`3b=d`( balancing `Mn` atoms)....(iv)
`12b=c+2d+4e+f`(balancing `O` atoms)....(v)
Combining eqautions (i) and (ii)
`6a=f=18e`
Combining eqautions (iii), (iv), and (v)
`12b=4d=12c=c+2d+4e+f`
Let `a=1`, then `f=6, 18e=6`, so `e=(1)/(3)`
From equation (v)
`4d=c+2d+4e+f`
`4d=(1)/(3)d+2d+4xx(1)/(3)+6`
`:. 4d-(1)/(3)d-2d=(4)/(3)+6`
`:. d=(22)/(5)`
Similarly from eqaution (v)
`12b= 4d= 4xx(22)/(5)=(88)/(5xx12)=(22)/(15)`
Hence, the coefficients are
`a=1, b(22)/(15), c=(1)/(3)d=(1)/(3)xx(22)/(5)=(22)/(15)`
`d=(22)/(5), e=(1)/(3), f= 6`
Multiply each of these values by `30` to obtain the intergral ratio
`a:b:c:d:e:f=30:44:44:132:10:180` ,brgt Hence, the balanced eqauiton is
`30Pb(N_(3))_(2)+44Co(MnO_(4))_(3)rarr44CoO+132MnO_(2)+10Pb_(3)O_(4)+180NO`
c.
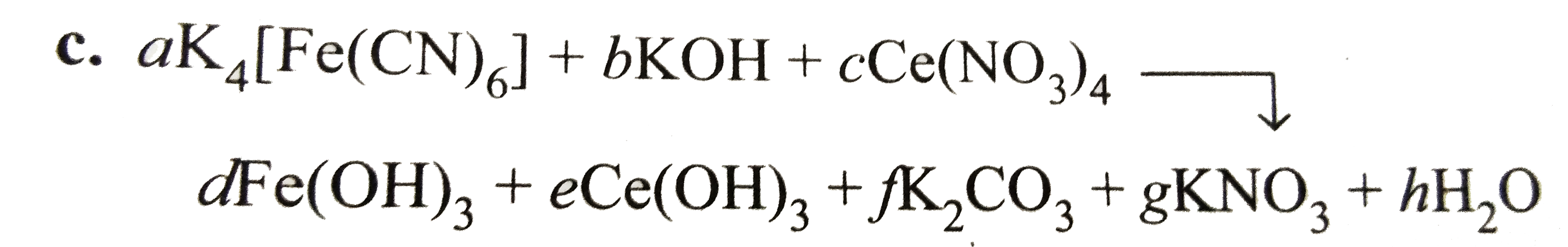
`:. 4a+b=2f+g`(balancing `K` atom).....(i)
`a=d`(balancing `Fe` atoms)....(ii)
`6a=f`(balancing `C` atoms).....(iii)
`6a+4c=g`(balancing `C` atoms).....(iv)
`b+12c=3d+3e+3f+3g+h` (balancing `O` atoms)....(v)
`b=3d+3e+2h` (balancing `H` atoms)....(vi)
Solve the eqaution and simplify to obtain the integral ratios.
`a:b:c:d:e:f:g:h=1:258:61:1:6:250:36`
Hencek the complete equaiton is
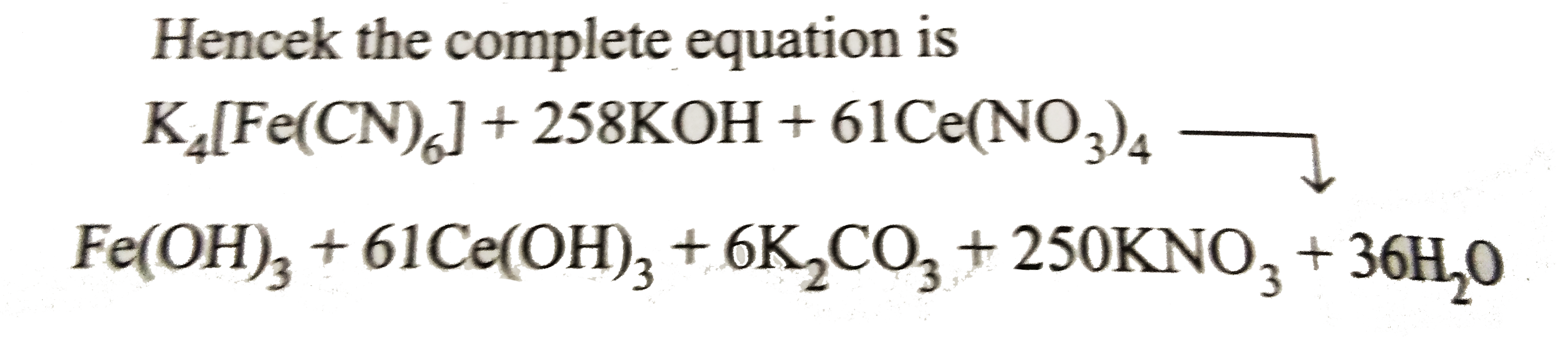
.
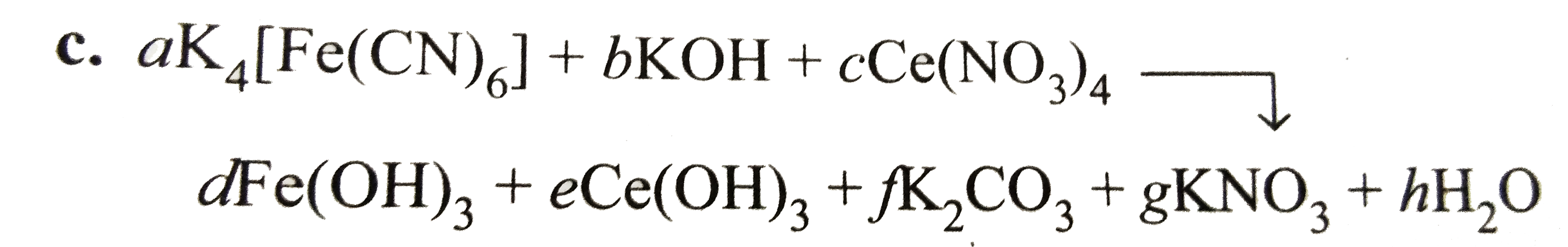
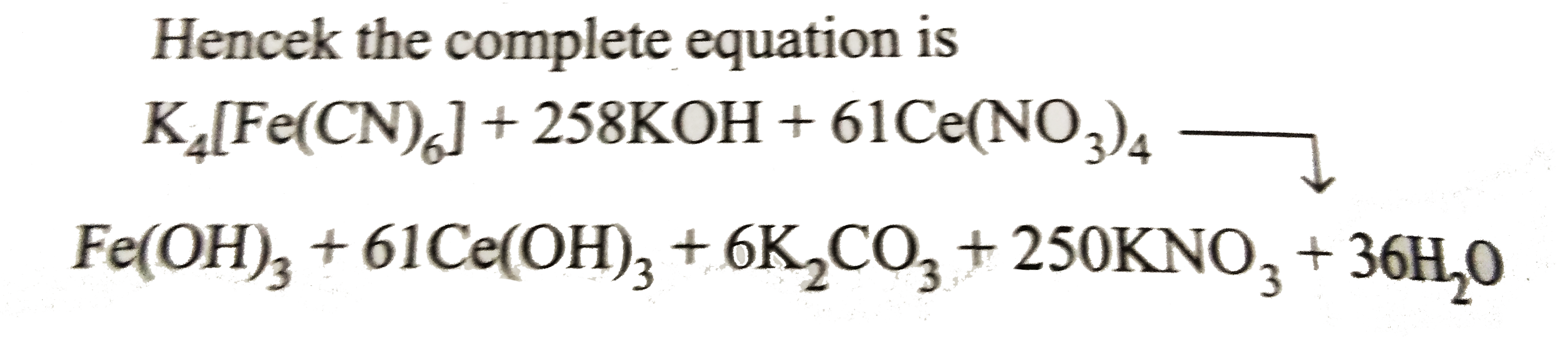 .
.