Home
Class 10
MATHS
In DeltaPQR, seg XY|| side QR. M and N a...

In `DeltaPQR`, seg `XY||` side `QR`. `M` and `N` are the midpoints of seg `PY` and side `PR` respectively, `P-M-Y-N-R`.
Prove that `(i) DeltaPXM~DeltaPQN`
`(ii)` seg `XM||` seg `QN`.

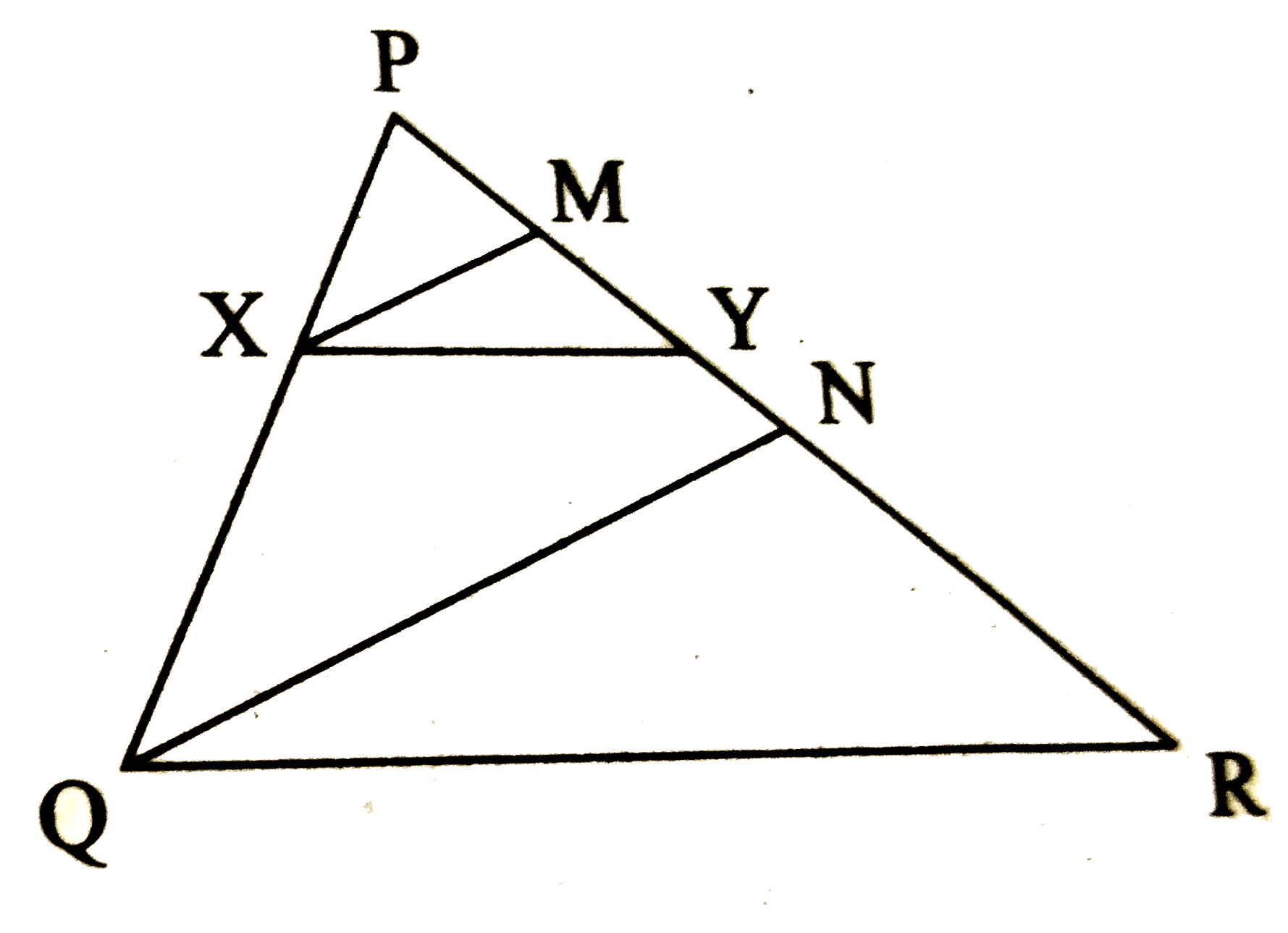
Text Solution

Verified by Experts

In `DeltaPXY` and `DeltaPQR`,
`/_PXY~=/_PQR`……(Seg `XY||` side `QR`, corresponding angles)
`/_XPY~=/_QPR`…..(Common angle)
`:.DeltaPXY~DeltaPQR`……("AA"test for similarity)
`:.(PX)/(PQ)=(PY)/(PR)`………..(c.s.s.t)…….`(1)`
Point `M` and `N` are the midpoints of seg `PY` seg `PR` respectively. .......(Given)
`:.PY=2PM` and `PR=2PN`........`(2)`
`:.(PX)/(PQ)=(2PM)/(2PN)`.....[From `(1)` and `(2)`]
`:.(PX)/(PQ)=(PM)/(PN)` ........`(3)`
In `DeltaPXM` and `DeltaPQN`,
`(PX)/(PQ)=(PM)/(PN)` [From `(3)`]
`/_XPM~=/_QPN`.......(Common angle)
`:.DeltaPXM~DeltaPQN` ......(SAS test for similarity)
`:./_PXM=/_PQN`........(c.a.s.t)
`:.` seg `XM||` seg `QN`.........(Corresponding angles test for parallel lines)
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • SIMILARITY

    NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise EXAMPLE TYPE|50 Videos

  • SIMILARITY

    NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise CHALLENGING QUESTIONS|8 Videos

  • SIMILARITY

    NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise 2.4 (3 mark each)|8 Videos

  • QUADRATIC EQUATIONS

    NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise ASSIGNEMENT 2.4|8 Videos

  • STATISTICS

    NAVNEET PUBLICATION - MAHARASHTRA BOARD|Exercise EXAMPLES FOR PRACTICE (MCQs)|35 Videos

Similar Questions

Explore conceptually related problems

In DeltaPQR, set XY|| sides QR, M and N are midpoints of seg PY and seg PR respectively. Prove that: (i) DeltaPXM~DeltaPQN (ii) "seg"XM||"sec"QN .

In A PQR, if PQ=PQ and L,M and N are the mid-points of the sides PQ,PR and RP respectively.Prove that LN=MN

Knowledge Check

  • Let square PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=

    A
    `3overline(MN)`
    B
    `4overline(MN)`
    C
    `2overline(MN)`
    D
    `2overline(NM)`

  • OPQR is a square and M, N are the middle points of the sides PQ and QR respectively, then the ratio fo the areas of the square and Delta OMN is

    A
    `4:1`
    B
    `2:1`
    C
    `8:3`
    D
    `4:3`

  • OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is

    A
    ` 4: 1`
    B
    ` 2 : 1`
    C
    ` 8 : 3`
    D
    ` 4 : 3`

    • Similar Questions

    Explore conceptually related problems

    In Delta P Q R , if P Q=Q R and L ,M and N are the mid-points of the sides P Q ,Q R and R P respectively. Prove that L N=M Ndot

    In the figure, M and N are the midpoints of sides PQ and PR respectively . If MN =6 cm then find QR. State your reason .

    M and N are the points on sides QR and PQ respectively of a trianglePQR , right angled at Q. prove that PM^(2) + RN^(2)= PR^(2)+MN^(2)

    In DeltaABC,L,M,N are points on side AB,BC,AC respectively. Perpendiculars drawn at L,M,N form DeltaPQR . Prove that DeltaABC~DeltaPRQ .

    Let D(x_(4),y_(4)) be a point such that ABCD is a square and M and P are the midpoints of the sides BC&CD respectively,then

    Home
    Profile