Velocity -time graph and acceleration-time graph are as shon in figs. and .

.

.
Analysis of motion
a. Between points `A` and `B`: Between these points, `x` has negative value, it means the particle is to the left of the origin. But the value of `x` is decteasing , so the particle is moving towards the origin. It means the velocty of particle is positives.
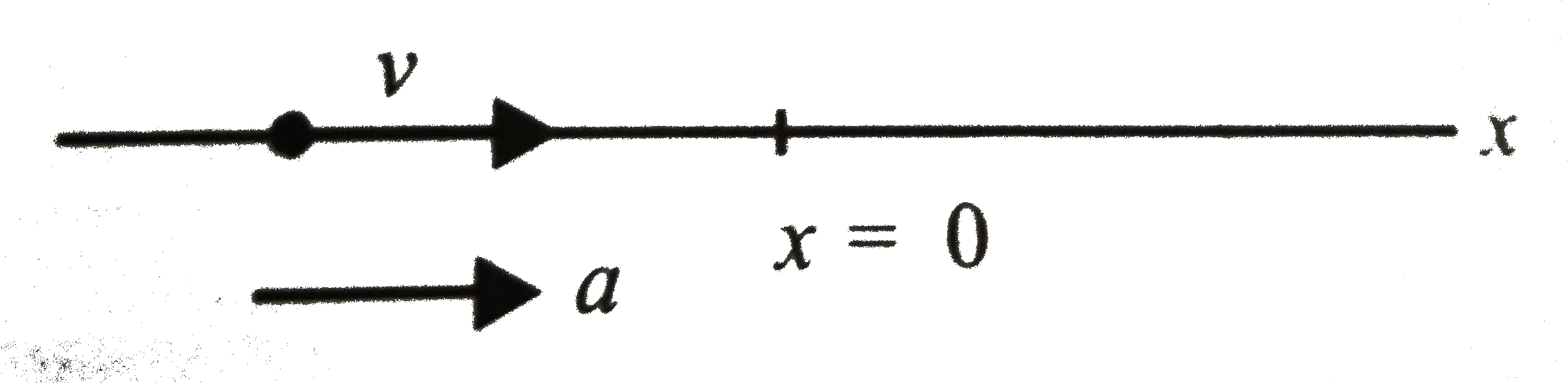
.
Between these points, the slope of the `x-t` graph is increasing, it means the magnitude of velocity is increasing. It means the velocity and acceleration both are in the same dirction. So acceleration is positiove. Note that acceleration is constant between `A` and `B`.
b. At out `B`: Porticle is at origin at this point. At this point, the slope of the `x-t` fraph is maximum so velocity is maximum at this point. Before point `B`, acceleration is positive, but aftre point `B` acceleration eill be negative as the slope of the `x-t` graph eill stat decrereasing after this,

.
We cannot define acceleration at point `B`.
c. Between points `B` and `C`: Between these points, `x` has positive value, it means the particle is to the right of the origin . But the value of `x` is increasing, so the particle is moveing away from the origin. It means the velocity of the paarticle is positive.

.
Between these points, the slope of the `x-t` fraph is decreasing, is means the magnitude of velocity is dectrasing. It means the velocity and acceleration are in opposite directions. So the between `B` and `C`.
Also the fraph is concave down, so acceleration is negative.
d. At point `C`: Particle is maximum away the origin at this point. At this point, the slope of the `x-t` graph zero, so velocity is zero. But acceleration is negative as the graph is concave down. at this point, the particle will change its direction of motion.

.
So after this, the particle will start moving towards the origin.
e. Between poinsts `C` and `D` : Between these points `x` has positive value, it means the particle is to the to right of the origin. But the value of `x` is decreasing so the particle is moving towards the origin. It means the velocity of the particle is negative.

.
Between these points, the magnitude of slope of the `x-t` graph is increasing, it means the magniude of velocity is increasing, but in the negative direction. so acceleration is negative. Note that acceleration is constant between `c` and `D`,
Alos the graph is concave down, so acceleration is negative.
f. At point `D`: Particle is to the right of the origin of the origin at this point. At this point, the slope of the `x-t` graph is negative maximum, so veloity is maximum at this point in the neative direction. Before point `D`, acceleration is negative, but after point `D`, acceleration will be positive (as the graph is concave up after `D`. We cannot define acceleration at point `D`.
f. Between points `D` and `E`: Between these point, `x` has positive value, it means the particle is to the right of the origin. But the value of `x` is decreasung, so the particle is moving towards the origin. It means the velocity of the particle is negative.
Between these points, the magnitude of the slope of the `x-t` gragh is decteasing, it means the magnitude of velocity is decreasing, but in the negative direction. So acceleration is positive. Note graph is concave up, so acceleration is positive.
 .
. .
.  .
.  .
.  .
.  .
.  .
.  .
.