Constraint relation. Approach 1
We can observe that the wedge M can only move in horizontal direction towards left, and the block m can slide on inclined surface of M always in contact with the wedge.
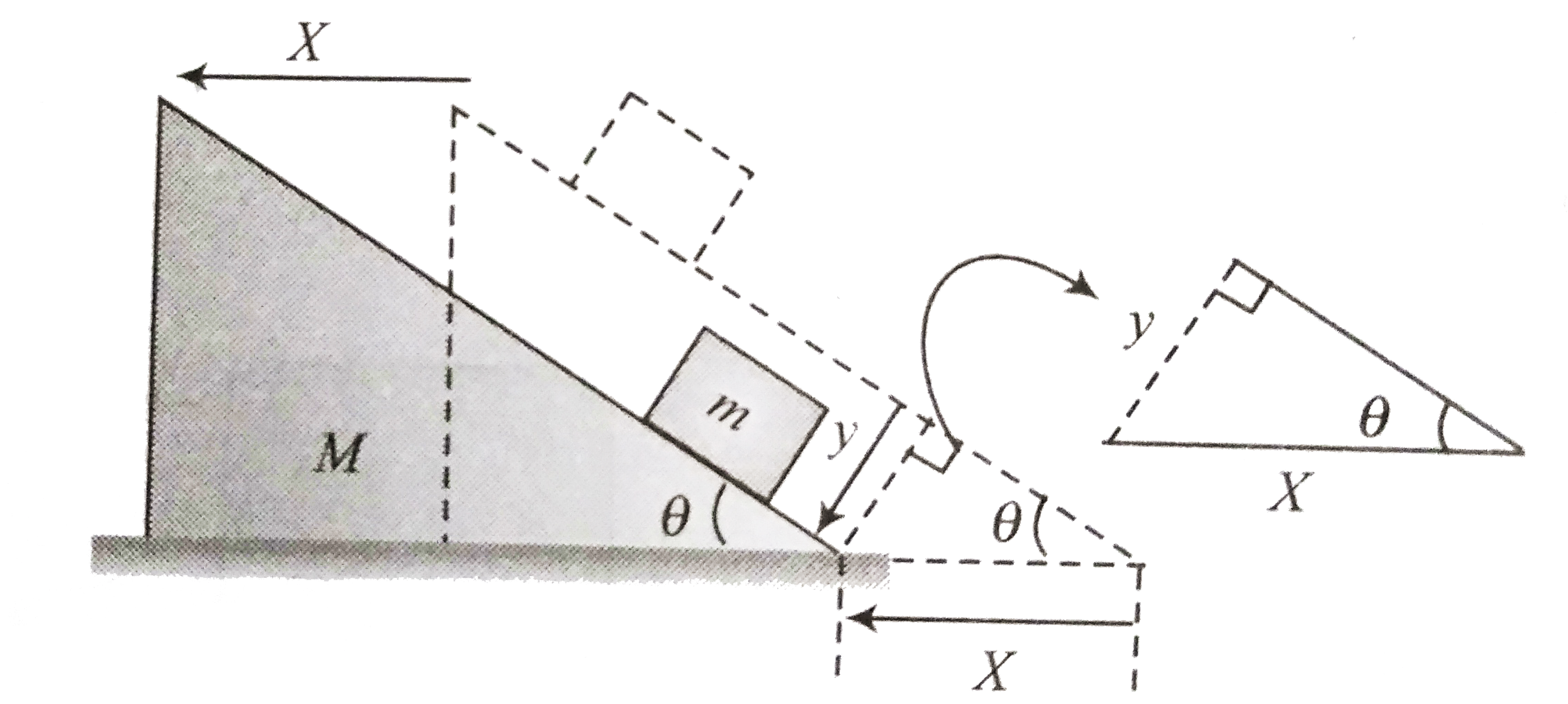
`*` Let us define our x and y axes parallel to the incline and perpendicular to incline. respectively.
`*` We can observe that the dispalcement of m and M in `-x'` direction will be same as the block never lose contact with the wedge.
`*` If the wedge moves in the horizontal direction by a distance x', during this time, the block will move x in x' direction.
`*` We can relate these displacement x and X as
`y/X = sin thata implies y=X sin theta` ..(i)
Hence, velocity relation can be written as :
`vy=V sin theta` ..(ii)
and acceleration relation can be written as:
`v_(x)=A sin theta` ..(iii)
Here `v_(y)` and `a_(y)` are the velocity and acceleration of the block, respectively, in the direction perpendicular to inclined surface.
Approach 2: We consider the motion of the block parallel to incline and perpendicular to inclined surface. Let the components of acceleration of block with respect to ground along these direction are `a_(x)` and `a_(y)` respectively.
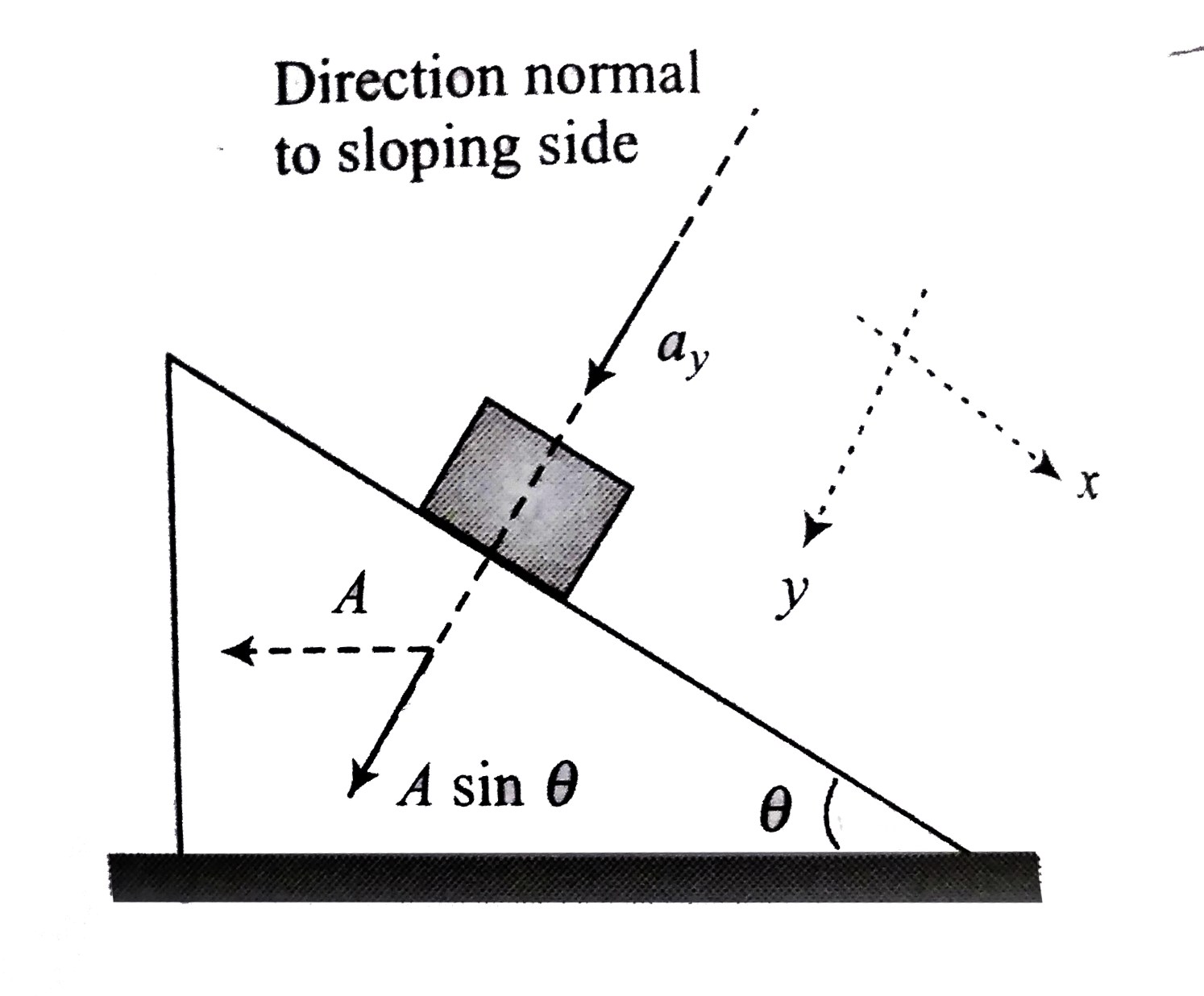
Then we can write `a_(y)=A sin theta`
For wedge:
`N sin theta=MA`...(i)
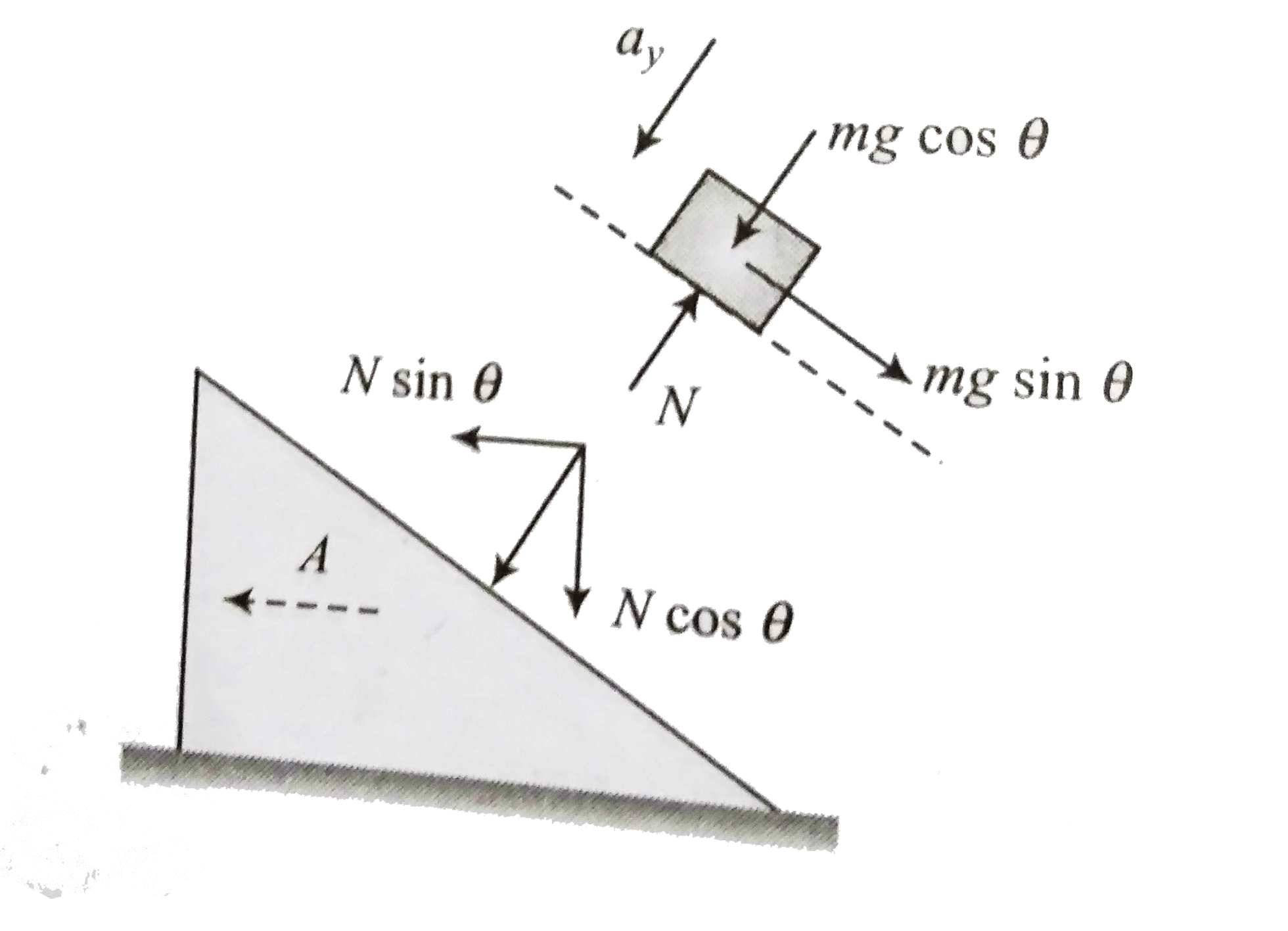
For block: Considering the block in the direction perpendicular to sloping surface.
`mg cos theta-N=ma_(y)`
but `a_(y)=A sin theta`
Hence, `mg cos theta-N=mA sin theta` ...(ii)
From (i) and (ii), we get
`A=(mg sin theta cos theta)/(M+m sin^(2)theta)`.



