The rod is constrained to move in the vertical direction (with the help of the guids) and the wedge will move along the surface in the horizontal direction. Initially, the system is held at rest.
Constraint relation: Approach 1 Let the acceleration of m w.r.t gound be a vertically downwards and acceleration of M w.r.t ground be A horizontally towards right.
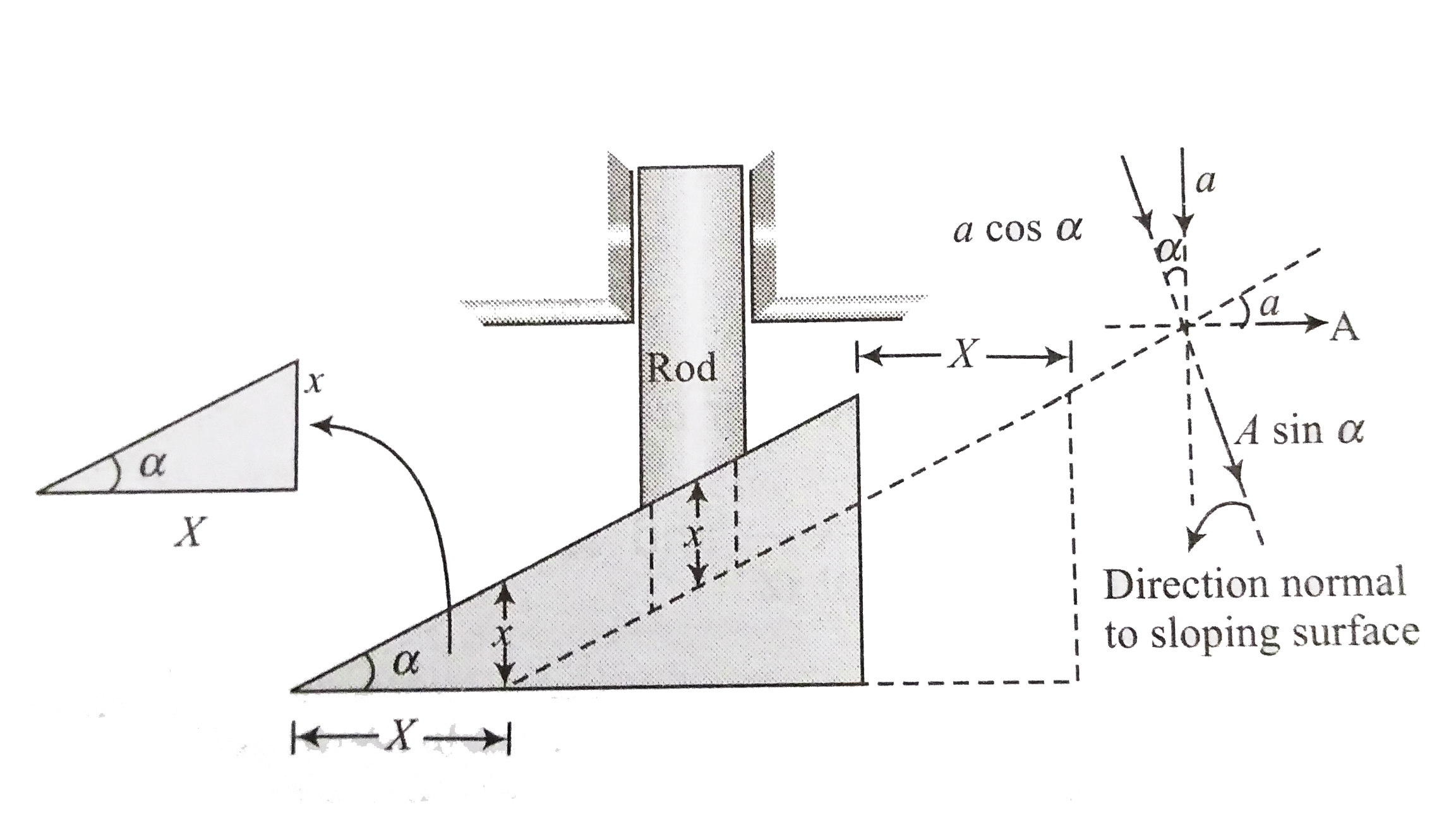
The motion of the system is constrained by the fact that the "bottom face of the rod must always be in contact with the inclined plane. If in time t, X is the displacement of the wedge and x is the displacement of the rod, then the constraint demands that
From fig. we have `x/X = tan alpha`
`:. x=X tan alpha` ...(i) Here `alpha` remains constant.
Differentating (i) w.r.t twice, we get
`((d^(2)x)/(dt^(2)))=((d^(2)X)/(dt^(2)))tan alpha` [`tan alpha = "constant"`]
Hence, `a=A tan alpha`
Approch 2: The fact that the rod (or a particle on the wedge and the wedge must not lose contact is usually called wedge constraints. For this, the component of the acceleration of the rod perpendicular to the wedge plane = component of acceleration of the wedge perpendicular to wedge plane.
`a cos alpha = A sin alpha implies a=A tan alpha`
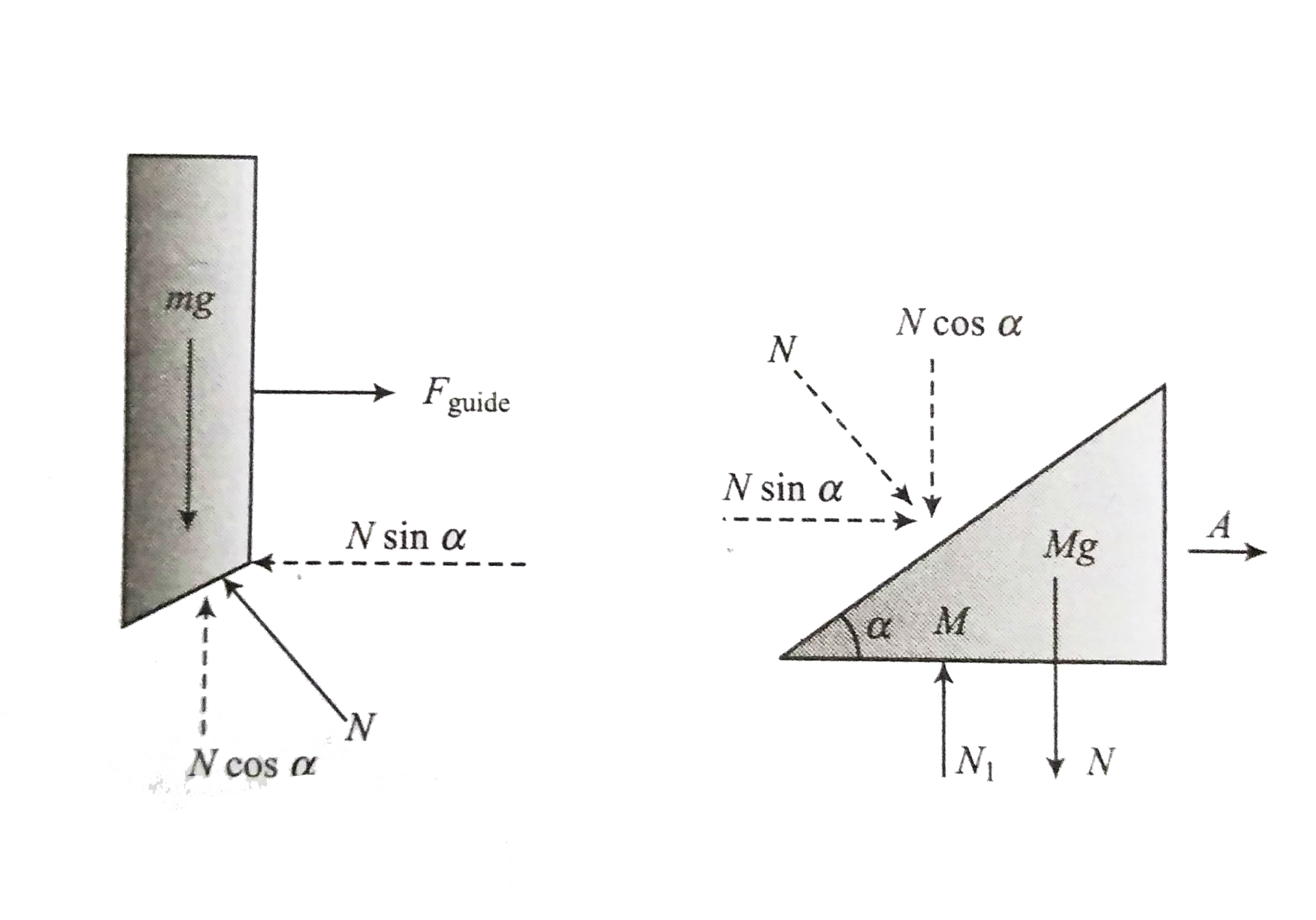
The force acting on the rod are:
,
`**` The weight mg, vertically downwars
`**` The normal force N, normal to the bottom surface of the horizontal component of N as for the rod `a_("horizontal")=0`.
Motion in vertical direction
`mg-N cos alpha=ma`...(ii)
and the force acting on the wedge are
`*` The weight, Mg
`**` N, reaction of N acting on the rod
`** N_(1)`, Normal force by the surface
The force equation are
`N_(1)-Mg -N cos alpha =0` ...(iii)
and `N sin alpha =MA` ...(iv)
Solving the above equation for a and A, we get
`a=(mg tan alpha)/(m tan alpha +N cot alpha)` and `A(mg)/(m tan alpha+M cot alpha)`.


 ,
,