A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
NEWTON'S LAWS OF MOTION 1
CENGAGE PHYSICS|Exercise Assertion-reasoning|15 VideosNEWTON'S LAWS OF MOTION 1
CENGAGE PHYSICS|Exercise Linked Comperhension|46 VideosNEWTON'S LAWS OF MOTION 1
CENGAGE PHYSICS|Exercise Single Correct|76 VideosMISCELLANEOUS VOLUME 2
CENGAGE PHYSICS|Exercise INTEGER_TYPE|10 VideosNEWTON'S LAWS OF MOTION 2
CENGAGE PHYSICS|Exercise Integer type|1 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-NEWTON'S LAWS OF MOTION 1-Multiple Correct
- A block of mass 30 kg is suspended by three string as shown in fig, Fi...
Text Solution
|
- In fig., a man true mass M is standing on a weighing machine placed in...
Text Solution
|
- The string in fig. is passing over small smooth pulley rigidly attache...
Text Solution
|
- Figure shown a block of mass m placed on a smooth wedge of mass M. Cal...
Text Solution
|
- The ring shown in fig. is given a constant horizontal acceleration (a(...
Text Solution
|
- In fig. a small block is kept on m. then
Text Solution
|
- A block of mass m is placed in contact with one end of a smooth tube o...
Text Solution
|
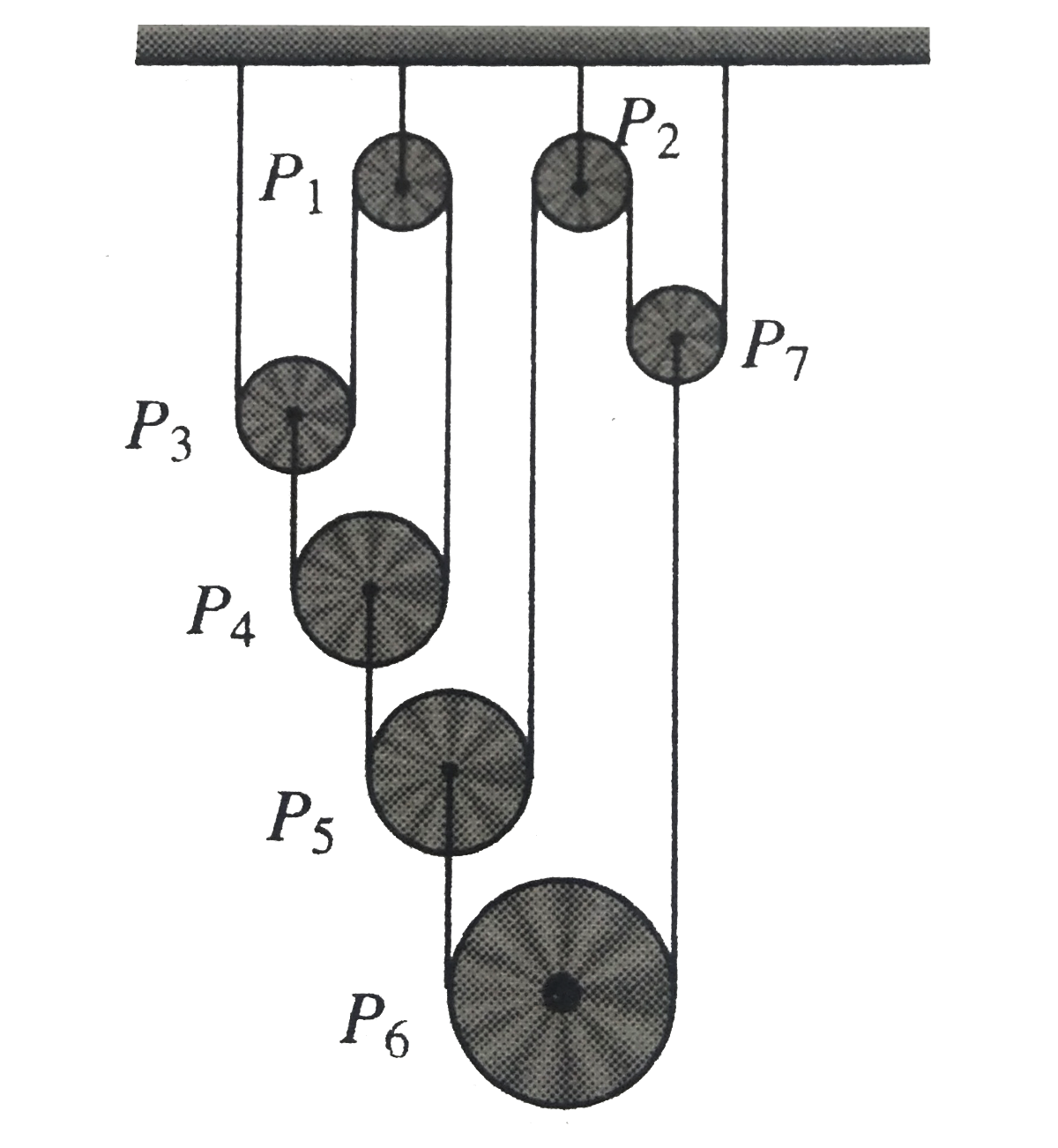
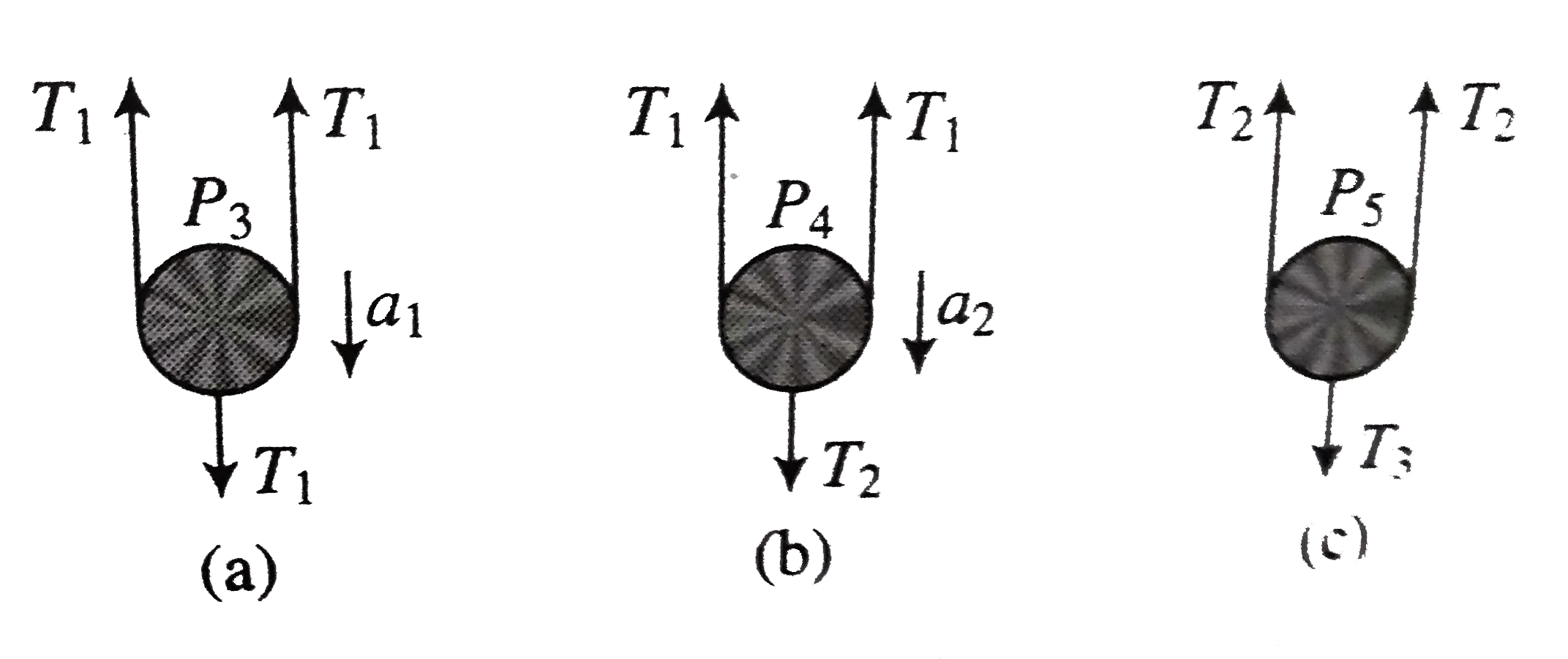
- Seven pulleys are connected with the help of three light string as sho...
Text Solution
|
- A block of mass m is placed on a wedge The wedge can be accelerated in...
Text Solution
|
- Two frame S(1) and S(2) are non-inertial. Then frame S(2) when observe...
Text Solution
|
- In fig the blocks A,B,and C of mass m each have acceleration a(1),a(2)...
Text Solution
|