Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-RIGID BODY DYNAMICS 1-Integer
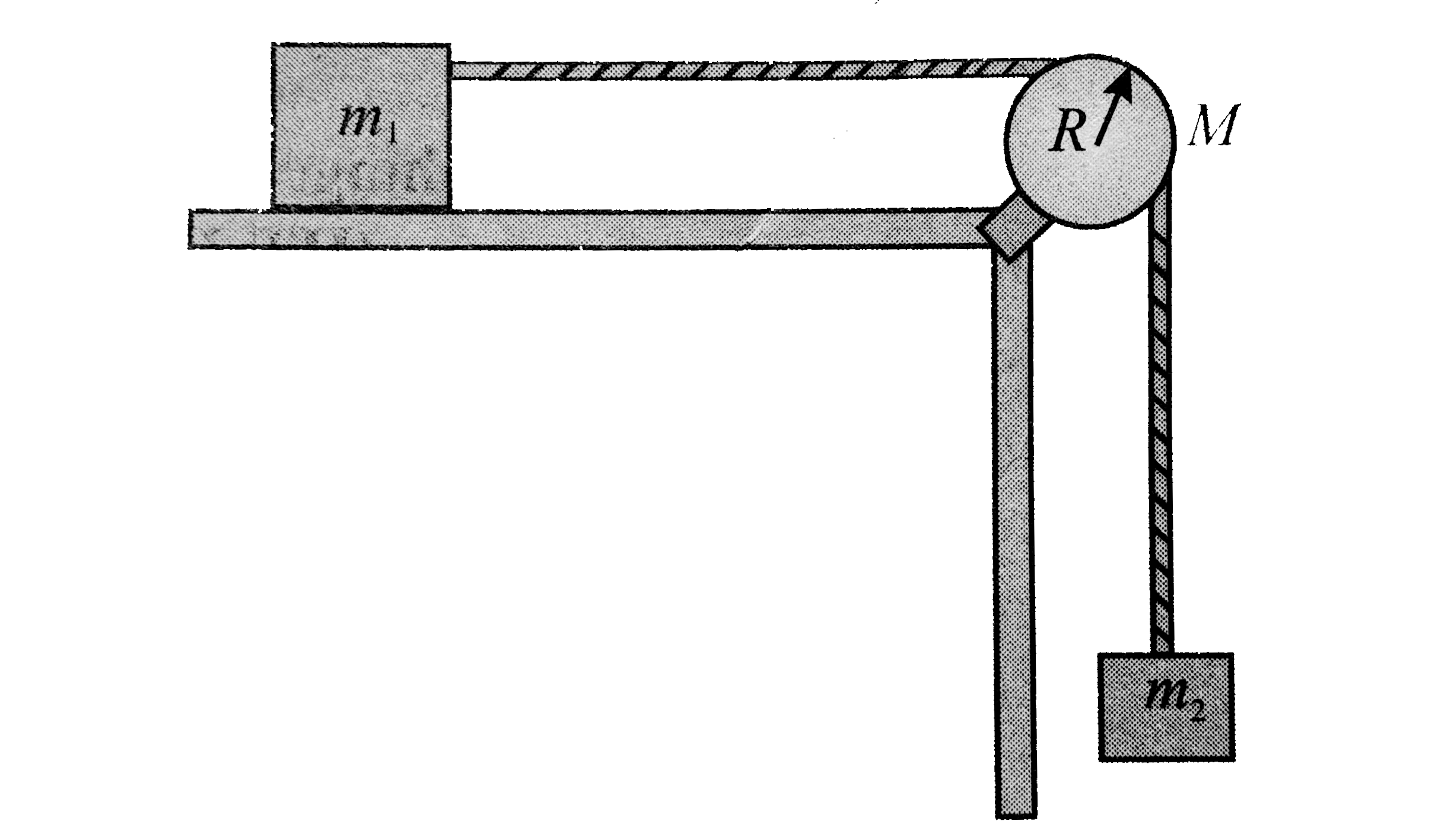
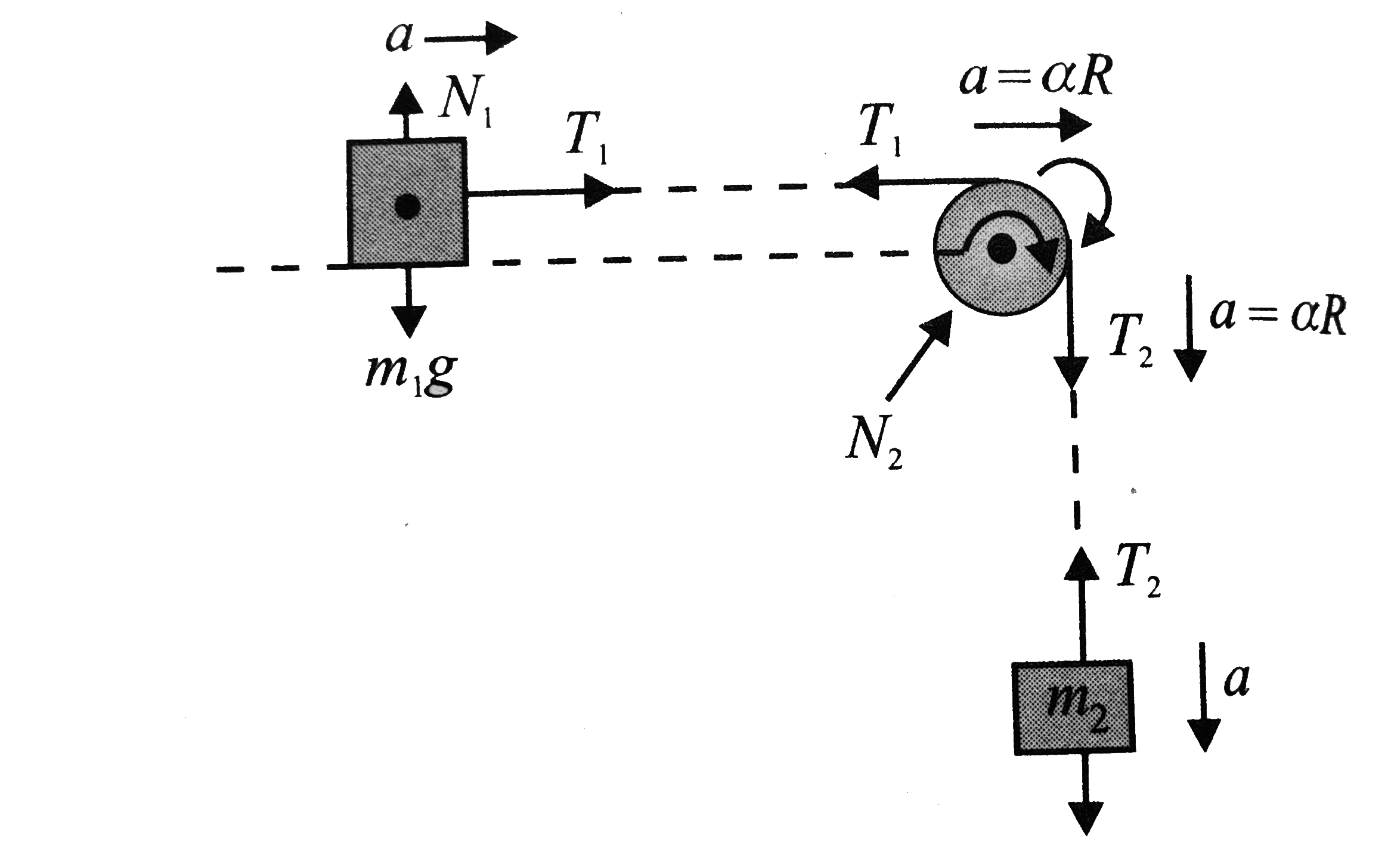
- In figure mass m(1) slides without friction on the horizontal surface,...
Text Solution
|
- A solid cylinder with r= 0.1 m and mass M = 2 kg is placed such that i...
Text Solution
|
- A uniform rod of length 1 m and mass 2 kg is suspended. Calculate tens...
Text Solution
|
- A uniform rod AB of mass 2 kg is hinged at one end A. The rod is kept ...
Text Solution
|
- A square plate ABCD of mass m and side l is suspended with the help of...
Text Solution
|
- Four solid spheres each of diameter sqart5cm and mass 0.5 kg are place...
Text Solution
|
- A uniform cylinder rests on a cart as shown. The coefficient of static...
Text Solution
|
- A uniform disc of mass m, radius R is placed on a smooth horizontal su...
Text Solution
|
- A uniform disc of mass m, radius R is placed on a smooth horizontal su...
Text Solution
|
- A uniform disc of mass m, radius R is placed on a smooth horizontal su...
Text Solution
|
- A light rigid rod of length 4 m is connected rigidly with two identica...
Text Solution
|
- A light rigid rod of length 4 m is connected rigidly with two identica...
Text Solution
|