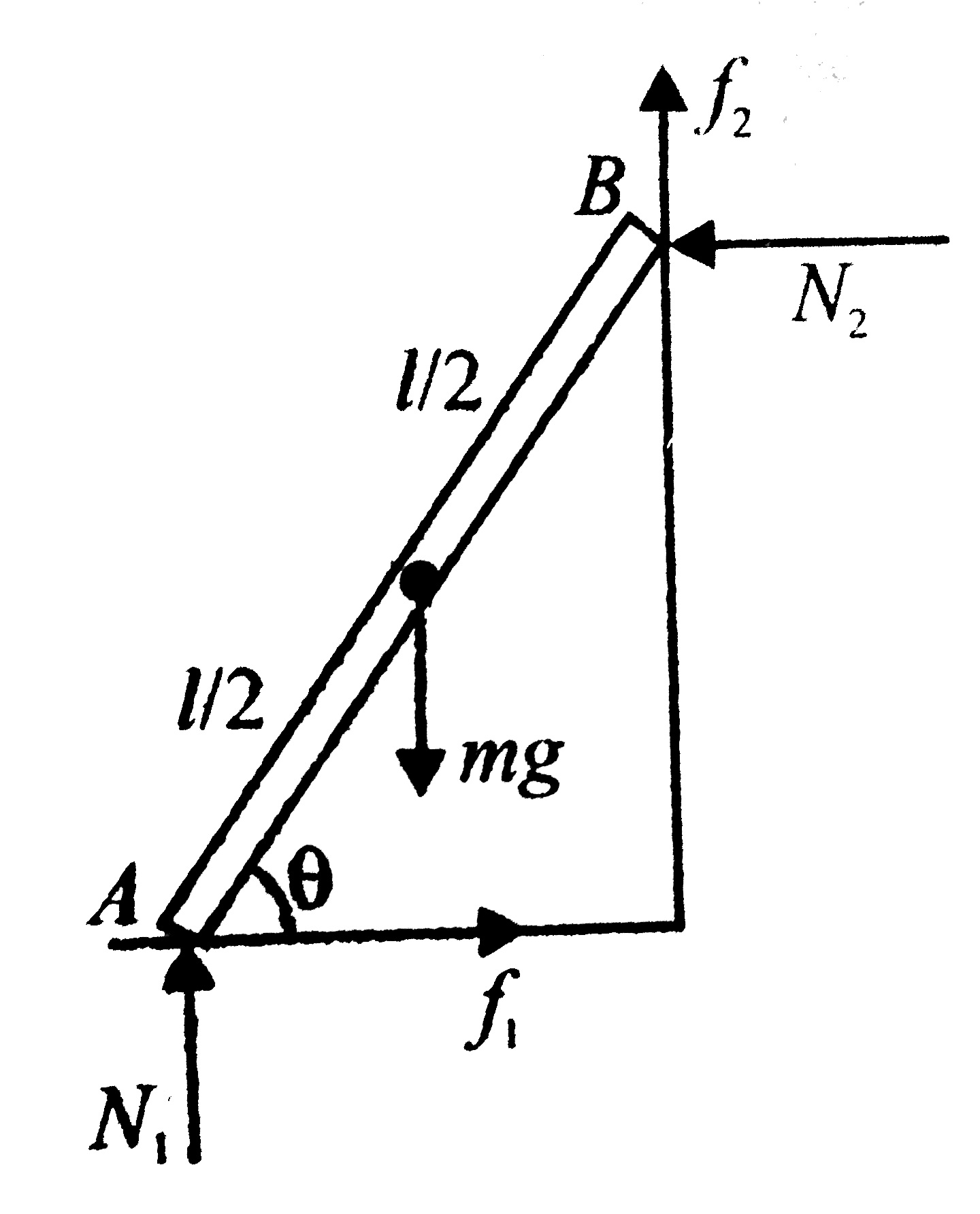Text Solution
Verified by Experts
Topper's Solved these Questions
RIGID BODY DYNAMICS 1
CENGAGE PHYSICS|Exercise Exercise 2.4|11 VideosRIGID BODY DYNAMICS 1
CENGAGE PHYSICS|Exercise Subjective|13 VideosRIGID BODY DYNAMICS 1
CENGAGE PHYSICS|Exercise Exercise 2.2|17 VideosPROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS|Exercise INTEGER_TYPE|2 VideosRIGID BODY DYNAMICS 2
CENGAGE PHYSICS|Exercise Interger|2 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-RIGID BODY DYNAMICS 1-Exercise 2.3
- A uniform cube of side a and mass m rests on a rough horizontal table....
Text Solution
|
- A uniform rod is made to lean between a rough vertical wall and the gr...
Text Solution
|
- A beam of weight W supports a block of weight W. The length of the bea...
Text Solution
|
- A uniform ladder of mass 10 g leans against a smooth vertical wall mak...
Text Solution
|
- A uniform ladder of length 10.0 m and mas 16.0 kg is resting against a...
Text Solution
|
- A uniform rod of length L rests against a smooth roller as shown in fi...
Text Solution
|
- The ladder shown in figure has negligible mass and rests on a friction...
Text Solution
|
- A uniform rod of length l and mass m is hung from, strings of equal le...
Text Solution
|
- A uniform ladder of length L and mass m(1) rests against a frictionles...
Text Solution
|
- A uniform beam of mass m is inclined at an angle theta to the horizont...
Text Solution
|
- A uniform rod of weight F(g) and length L is supported at its ends by ...
Text Solution
|
- Figure shows a vertical force applied tangentially to a uniform cylind...
Text Solution
|
- A trailer with loaded weightF(g) is being pulled by a vehicle with a f...
Text Solution
|
- A bicycle is traveling downhill at a high speed. Suddenly, the cyclist...
Text Solution
|
- A car moves with speed v on a horizontal circular track of radius R. A...
Text Solution
|