Home
Class 11
PHYSICS
Water flows out of a big tank along a tu...

Water flows out of a big tank along a tube bent at right angles, the inside of the tube is of radius `r`. The length of the horizontal portion is `l`. The rate of water flow is `Q`. Find the moment of reaction forces of flowing water, acting on the tube walls relative to point `O`.

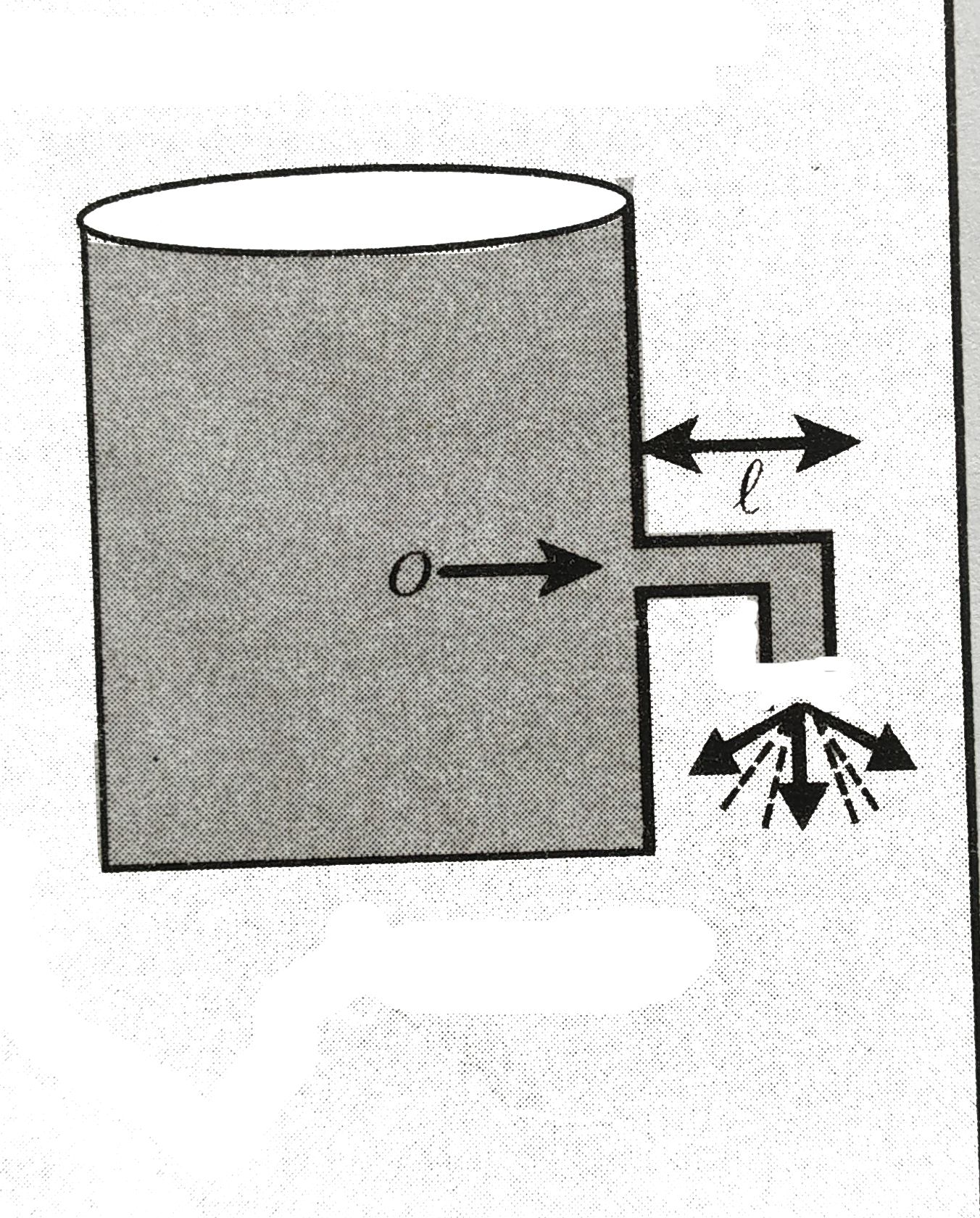
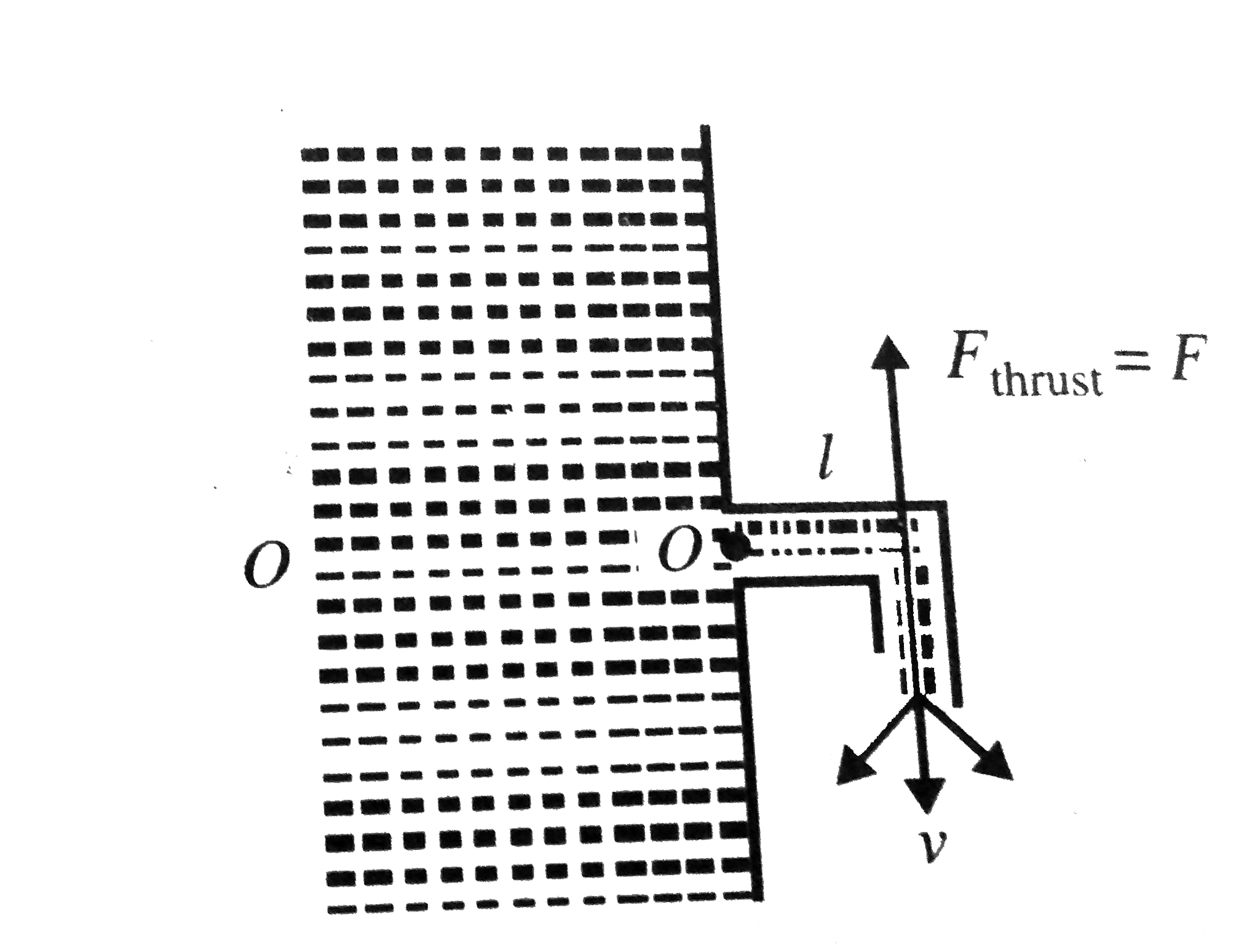
Text Solution

Verified by Experts


Velocity of flow `=v=Q/(pir^(2))`
Reaction force `F=rhoAv^(2)`
`impliesF=rhopir^(2)(Q/(pir^(2)))^(2)=(Q^(2))/(pir^(2))rho`
Torque about `O+Fl=(Q^(2)rhol)/(pir^(2))`
Promotional Banner

Topper's Solved these Questions

  • FLUID MECHANICS

    CENGAGE PHYSICS|Exercise Subjective|25 Videos

  • FLUID MECHANICS

    CENGAGE PHYSICS|Exercise Single Correct|95 Videos

  • FLUID MECHANICS

    CENGAGE PHYSICS|Exercise Exercise 4.3|10 Videos

  • DIMENSIONS & MEASUREMENT

    CENGAGE PHYSICS|Exercise Integer|2 Videos

  • GRAVITATION

    CENGAGE PHYSICS|Exercise INTEGER_TYPE|1 Videos

Similar Questions

Explore conceptually related problems

Water flows out of a big tank along a tube bent at right angles, the inside radius of the tube is equal to r=0.50cm (figure). The length of the horizontal section of the tube is equal to l=22cm . The water flow rate is Q=0.50 litres per second. Find the moment of reaction forces of flowing water, acting on the tube's walls, relative to the point O.

Water is flowing through a tube of radius r with a speed v. If this tube is joined to another tube of radius r/2, what is the speed of water in the second tube?

Water flows with a velocity V in a tube of diameter d and the rate of flow is Q. another tube of diameter 2d is coupled to the first one. The velocity of water flowing out and rate of flow in the second tube are respectively.

A fluid is flowing through a tube of length L. The radius of the tube is r and the velocity of the fluid is v. If the radius of the tube is increased to 2r, then what will be the new velocity?

Water is flowing through a long horizontal tube. Let P_A and P_B be the pressures at two points A and B of the tube

Water flows through a capillary tube at the rate of 10 cc per minute. If the pressure difference across the same tube is doubled, the rate of flow of water throught he tube wil be (in cc per minute)

Water flows in a stream line manner through a capillary tube of radius a. The pressure difference being P and the rate of flow is Q. If the radius is reduced to a/4 and the pressure is increased to 4P. then the rate of flow becomes