Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROMAGNETIC INDUCTION
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)|Exercise Textual Exercise|18 VideosELECTRIC CHARGES AND FIELDS
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)|Exercise DAM SURE LAQ|1 VideosELECTROMAGNETIC WAVE
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)|Exercise ADDITIONAL EXERCISES|19 Videos
Similar Questions
Explore conceptually related problems
VIKRAM PUBLICATION ( ANDHRA PUBLICATION)-ELECTROMAGNETIC INDUCTION -Additional EXERCISES
- Suppose the loop in Textual Exercise 4 is stationary but the current f...
Text Solution
|
- A square loop of side 12 cm with its sides parallel to X and velocity ...
Text Solution
|
- It is desired to measure the magnitude of field between the poles of a...
Text Solution
|
- Following figure shows a metal rod PQ resting on the smooth ralls AH a...
Text Solution
|
- Following figure shows a metal rod PQ resting on the smooth ralls AH a...
Text Solution
|
- Following figure shows a metal rod PQ resting on the smooth ralls AH a...
Text Solution
|
- Following figure shows a metal rod PQ resting on the smooth ralls AH a...
Text Solution
|
- Following figure shows a metal rod PQ resting on the smooth ralls AH a...
Text Solution
|
- Following figure shows a metal rod PQ resting on the smooth ralls AH a...
Text Solution
|
- Following figure shows a metal rod PQ resting on the smooth ralls AH a...
Text Solution
|
- An air-cored solenoid with length 30 cm, area of cross-section 25 cm^(...
Text Solution
|
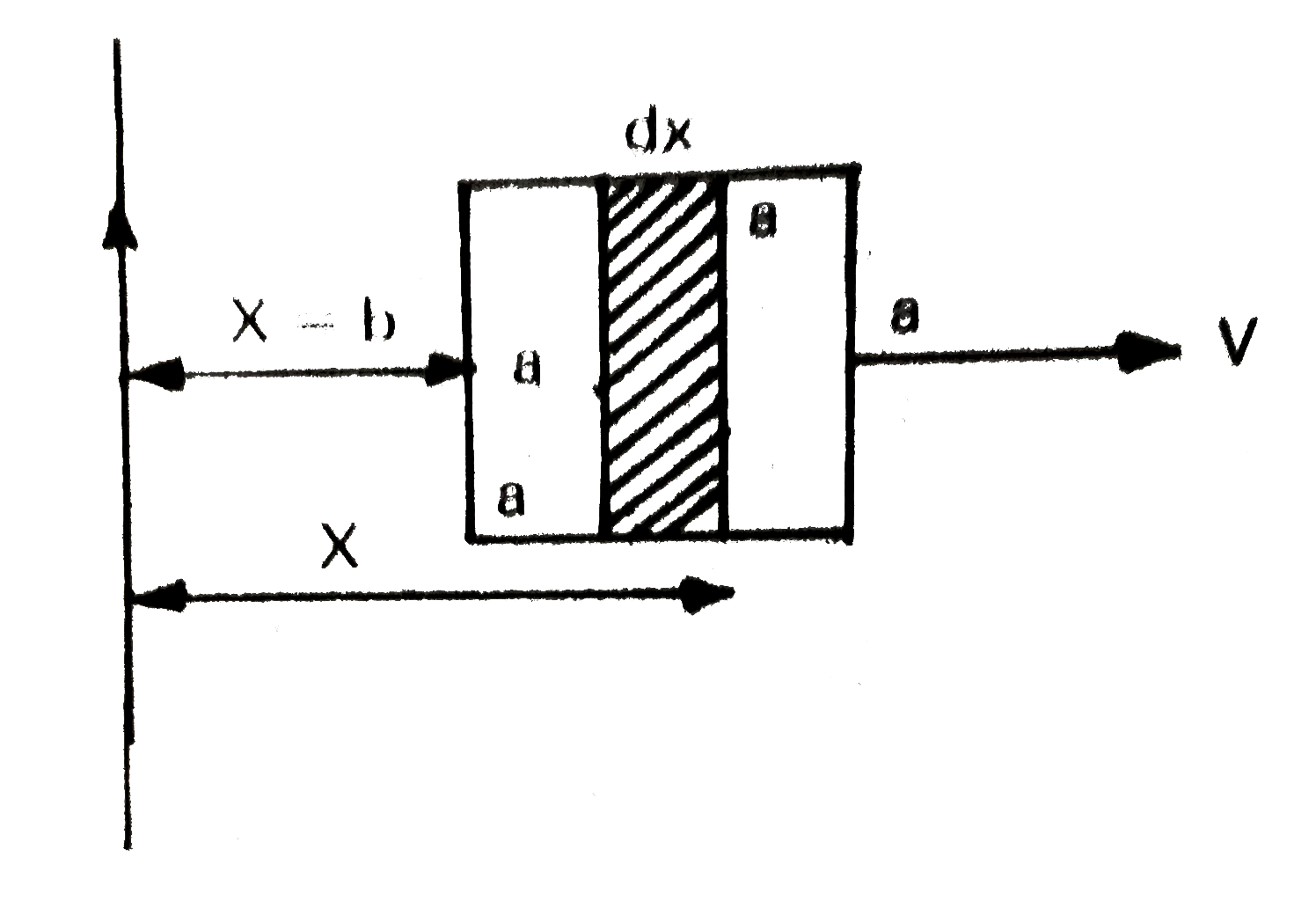
- Obtain an expression for the mutual inductance between a long straight...
Text Solution
|
- Now assume that the straight wire carries a current of 50A and the loo...
Text Solution
|
- A line charge lambda per unit length is lodged uniformly onto the rim ...
Text Solution
|
- Obtain an expression for the self inductance of a solenoid.
Text Solution
|