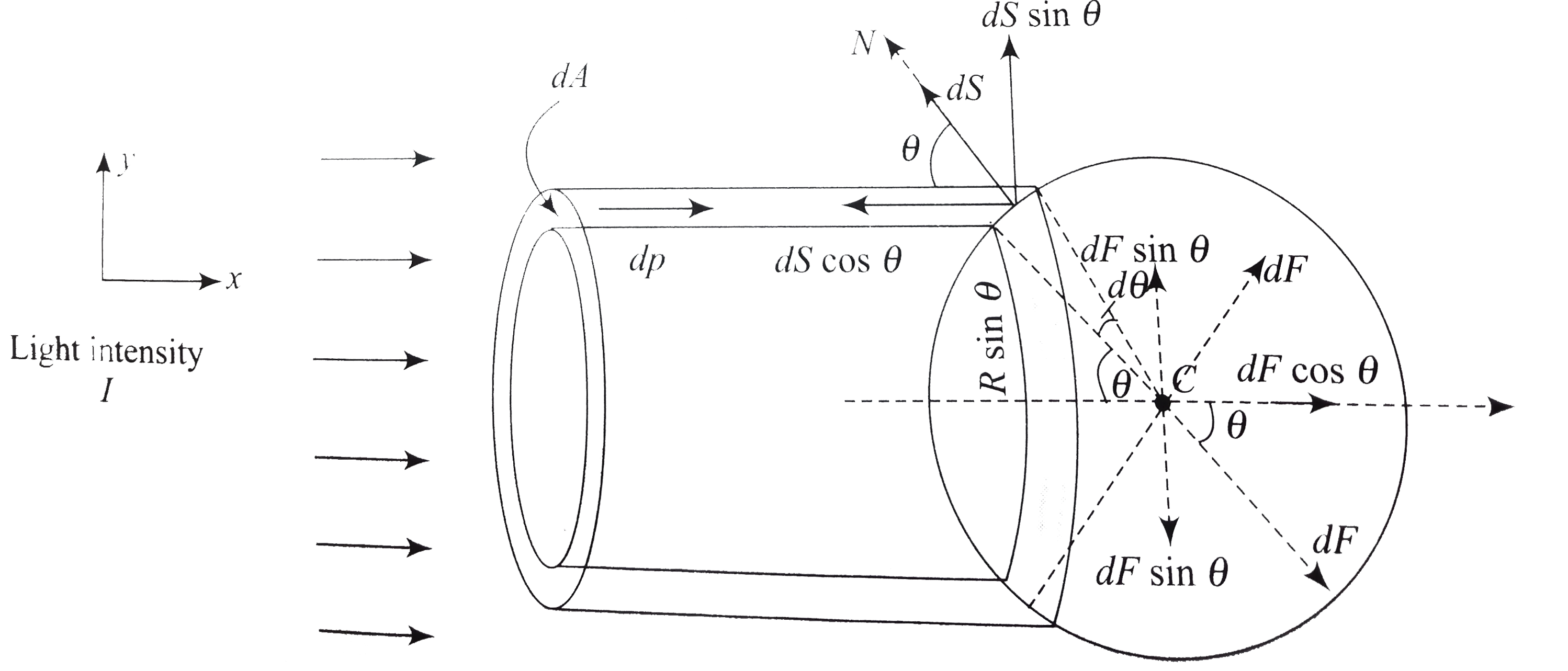
The front surface of the sphere will be illuminated by the light as shown in Fig as angle of incidence of light is different position of the front face of the sphere.
We can cosider a small elemental circular strip (ring) of angular width `dtheta` on its surface at an angle `theta` from its horizontal diameter as shown . Let the area of this elemental strip is dS, then
`dS=2thetaRsinthetaRd` `theta`...(i)
`Rsintheta` is the radius of this circular strip (ring).
We take the projection of area of this slant elemental circular strip in vertical plane. Let dA be the projection of the slant strip area dS along the cross-sectional plane of the light beam and it is given as
`dA=dScostheta`....(ii)
Hence, the power of light incident on this strip is `dP=IdA`. The momentum of photons per second incident on this strip is `dA=(dP)/(c)=(IdA)/(c)`....(iii)
These photons are incident at an angle `theta` to the normal N of this strip. As the surface of the sphere is perfectly reflecting, the photons will be reflected at the same angle `theta` to N as shown in the figure.
Hence, the change in linear momentum of photons is along the normal and thus force exerted on this strip along the normal is
`dF=2dpcostheta=(2IdA)/(c)costheta`...(iv)
Thus, the net force on sphere will be along the x-axis only.
Thus, the force on the sphere will be given as
`FintdFcostheta=int(2IdA)/(c)cos^(2)theta`
`=int_0^((pi)/(2))(2I)/(c)(2piRsinthetacosthetaRd theta)cos^(2)theta`
`(4IpiR^(2))/(c)int_0^((pi)/(2))cos^(3)thetasinthetad theta=(4IpiR^(2))/(c)[-(cos^(4))/(4)]_0^((pi)/(2))`
`(IpiR^(2))/(c)[1-0]=(IpiR^(2))/(c)`...(v)
